(2003•哈尔滨)已知:抛物线y=ax2+bx+c经过A(1,0)、B(5,0)两点,最高点的纵坐标为4,与y轴交于点C.
(1)求该抛物线的解析式;
(2)若△ABC的外接圆⊙O’交y轴不同于点c的点D’,⊙O’的弦DE平行于x轴,求直线CE的解析式;
(3)在x轴上是否存在点F,使△OCF与△CDE相似?若存在,求出所有符合条件的点F的坐标,并判定直线CF与⊙O’的位置关系(要求写出判断根据);若不存在,请说明理由.
【答案】
分析:(1)根据A、B两点的坐标即可得出抛物线的对称轴解析式,也就可得出抛物线顶点的坐标,然后根据顶点、A、B这三个点的坐标即可求出的抛物线的解析式.
(2)本题的关键是求出E点的坐标,根据圆的对称性可知,D与E关于抛物线的对称轴对称.因此只需求出D点的坐标即可得出E点的坐标,那么首先要求出OD的长,已知了OA、OB、OC的长,可根据切割线定理求出OD的长,进而可得出D、E点的坐标,然后可根据C、E的坐标用待定系数法求出直线CE的函数解析式.
(3)求F点的坐标要分类进行讨论:
①当∠CED=∠CFO,即△CDE∽△COF,由于DE∥x轴,因此直线CE与x轴的交点就满足F点的条件,设此点为F1,F1关于y轴的对称点F2也符合这样的条件.
②当∠CFO=∠DCE时,即△CDE∽△FOC,可根据相似三角形得出的对应成比例线段求出OF的长,即可得出F点的坐标.(同①一样y轴左右各有一个符合条件的F点)
如图:可过O′作CF
3的垂线设垂足为H,由于∠HCO′是锐角,因此O′H<O′C,所以CF
3与圆O′的相交,同理可得出CF
1,DF
4也与圆O′相交.由于∠F
4CO=∠CED,而∠CED+∠DCE=90°,那么∠F
4CE=90°,因此只要CF4与圆O′相切,CF
1,CF
2,CF
3都与圆相交.
解答:(1)解:由对称性可知抛物线的最高点的横坐标是3,所以抛物线的最高点坐标为(3,4)
∴
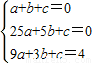
解得
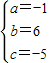
.
所以抛物线解析式为y=-x
2+6x-5.
(2)如图,∵C(0,-5),
∴OC=5,
∵OA•OB=OD•OC,
∴1×5=OD×5
∴OD=1
∵直线x=3垂直平分DE,
∴DE=6.
∵DE∥x轴,
∴E(6,-1)
设直线CE的解析式为y=kx+b.
∴
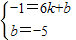
解得
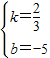
故直线CE解析式为y=

x-5.
(3)假设存在点F,使△CDE与△COF相似.
∵DE∥AB,
∴∠CDE=90°
∵∠COF=90°
∵∠CDE=∠COF∴△DCE∽△COF或△CDE∽△FOC
当△CDE∽△COF时,
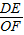
=
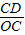
,所以OF=
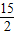
.
当△CDE∽△FOC时,
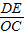
=
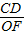
,所以OF=
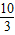
.
所以存在点F,使△CDE与△COF相似.其坐标为F
1(
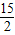
,0),F
2(-
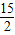
,0)
F
3(
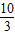
,0),F
4(-
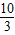
,0)
∵∠OCF
4=∠CED,
∴∠ECF
4=90°
所以直线CF
4与⊙O'相切
∵∠CDE=90°
∴直线CF
1经过圆心O′,
∴直线CF
1与⊙O'相交,
∴点F
3在线段OB上
∴∠F
3CE为锐角,做OH'⊥CF
3,垂足为H,所以O′H<O′C.
∴直线CF
3与⊙O′相交,同理直线CF
2与⊙O′相交.
故直线CF
4与⊙O′相切,直线CF
1、CF
2、CF
3都与⊙O′相交.
点评:本题主要考查了一次函数与二次函数解析式的确定、相似三角形的判定和性质、直线与圆的位置关系等知识点.

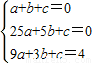
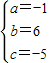 .
.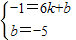
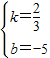
 x-5.
x-5.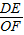 =
=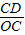 ,所以OF=
,所以OF=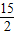 .
.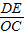 =
=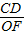 ,所以OF=
,所以OF=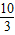 .
.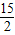 ,0),F2(-
,0),F2(-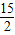 ,0)
,0)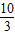 ,0),F4(-
,0),F4(-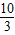 ,0)
,0)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
