
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:选择题
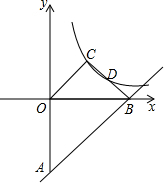 如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )
如图,直线y=x-4与y轴、x轴分别交于点A、B,点C为双曲线y=$\frac{k}{x}$上一点,OC∥AB,连接BC交双曲线于点D,点D恰好是BC的中点,则k的值是( )| A. | $\frac{16}{9}$ | B. | 2 | C. | 4 | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 若将三个数-$\sqrt{3}$,$\sqrt{6}$,$\sqrt{14}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{6}$.
若将三个数-$\sqrt{3}$,$\sqrt{6}$,$\sqrt{14}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,甲、乙两组同学去野外采集标本,他们从同一地点同时出发,各自沿固定的方向行走.当甲组行走600m、乙组行走630m时,两组的所在地相距870m,那么甲、乙两组同学行走的方向成多少度的角(即图中的α为多少度)?
如图,甲、乙两组同学去野外采集标本,他们从同一地点同时出发,各自沿固定的方向行走.当甲组行走600m、乙组行走630m时,两组的所在地相距870m,那么甲、乙两组同学行走的方向成多少度的角(即图中的α为多少度)?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,延长CD到点E,使DE=$\frac{1}{2}$CD,BE交AD于点F,则△DEF和△ABF的面积比为( )
如图,在?ABCD中,延长CD到点E,使DE=$\frac{1}{2}$CD,BE交AD于点F,则△DEF和△ABF的面积比为( )| A. | 1:4 | B. | 1:2 | C. | 1:3 | D. | 2:3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com