Question

“乡村小镇”饭店的大雅间是一个10米×7米房间，现只摆放着2套同样大小的圆桌和椅子，一套圆桌和椅子占据的地面部分可看成半径为1.5米的圆形，如图所示．有一位客人预定这个雅间，但是他需要请3桌客人，问领班能不能再加一套同样桌椅．假如你是领班，在保证通道最窄处的宽度不小于0.5米的前提下，你________（能或不能）摆下3套同样大小的圆桌和椅子．4套呢？________（能或不能）．

Answer 1

能    能
分析：我们把上面的格形图看作平面直角坐标系其中左下角为原点；则根据题目要求，下面一排桌子的中心最低在y=2上，才能满足下面的通道宽度≥0.5；而上面一排桌子的中心最高在y=5，才能满足上面的通道宽度≥0.5，而桌子的中心最左边为x=2，最右边为x=8．所以我们不妨设下面的一个桌子的中心为A（2，2），上面一个桌子的中心为B（b，5）．
|AB|²=（b-2）²+（5-2）²≥3.5²（b-2），进而求出符合要求的点的坐标．
解答：摆放三套与四套的设计方案参考示意图如下：

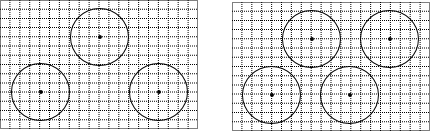
把上面的格形图看作平面直角坐标系其中左下角为原点；则根据题目要求，下面一排桌子的中心最低在y=2上，
才能满足下面的通道宽度≥0.5；而上面一排桌子的中心最高在y=5，才能满足上面的通道宽度≥0.5，而桌子的中心最左边为x=2，最右边为x=8．所以我们不妨设下面的一个桌子的中心为A（2，2），上面一个桌子的中心为B（b，5）．
|AB|²=（b-2）²+（5-2）²≥3.5²（b-2）．
所以可以摆下4个桌子，中心为A（2，2），B（4，5），C（6，2），D（8，5）．
故答案为：能，能．
点评：此题考查了圆与圆位置关系的运用，是开放性的题目，有一定的难度．