
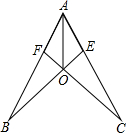
 如图,E,F分别在线段AB、AC上,BF、CE交于点O,连接OA,且OE=OF,添加一个条件________(不再添加其他字母或线段)
如图,E,F分别在线段AB、AC上,BF、CE交于点O,连接OA,且OE=OF,添加一个条件________(不再添加其他字母或线段) 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:013
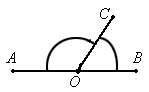
(2005福州课改)如图射线OC的端点O在线AB上,∠AOC的度数比∠BOC的2倍多10°.设∠AOC和∠BOC的度数分别为x、y,则下列正确的方程组为
[ ]
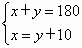
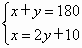
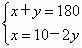
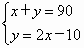
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
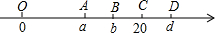
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《有理数》(01)(解析版) 题型:选择题
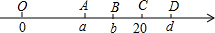
查看答案和解析>>
科目:初中数学 来源:2010年台湾省中考数学试卷(二)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com