
 .点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),∠OEF=∠A=∠DOC,设AE=t,OF=s.
.点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),∠OEF=∠A=∠DOC,设AE=t,OF=s.
 -
- t+10(0<t<12);
t+10(0<t<12); =
= =1,易求t值.
=1,易求t值.
 =8
=8 =
= =6
=6 .
. .b=16.
.b=16. x+16;(4分)
x+16;(4分)
 =
= .
. =
= ,100-10s=12t-t2,
,100-10s=12t-t2, -
- t+10(0<t<12);(3分)
t+10(0<t<12);(3分) (2分)
(2分) =
=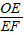 =1即OA=DE.12-t=10,t=2.
=1即OA=DE.12-t=10,t=2. 或t=2时△OEF是等腰三角形.(2分)
或t=2时△OEF是等腰三角形.(2分)

科目:初中数学 来源:2011年3月九年级质量评估数学试卷(解析版) 题型:解答题
 .点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),∠OEF=∠A=∠DOC,设AE=t,OF=s.
.点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),∠OEF=∠A=∠DOC,设AE=t,OF=s.
查看答案和解析>>
科目:初中数学 来源:2010年浙江省温州市六校联考中考数学三模试卷(解析版) 题型:解答题
 .点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),∠OEF=∠A=∠DOC,设AE=t,OF=s.
.点E、F分别是边AD和对角线OD上的动点(点E不与A、D重合),∠OEF=∠A=∠DOC,设AE=t,OF=s.
查看答案和解析>>
科目:初中数学 来源:2010年浙江省温州市六校联考中考数学三模试卷(解析版) 题型:填空题
 (x>0)的图象上,斜边OA1、A1A2、A2A3…An-1An都在x轴上.则点A10的坐标是 .
(x>0)的图象上,斜边OA1、A1A2、A2A3…An-1An都在x轴上.则点A10的坐标是 .
查看答案和解析>>
科目:初中数学 来源:2011年江苏省苏州市中考数学模拟试卷(一)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com