【答案】
分析:(1)把点A(m-4,0)和C(2m-4,m-6)代入直线y=-x+p上得到方程组
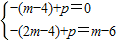
,求出方程组的解
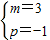
,得出A、B、C的坐标,设抛物线y=ax
2+bx+c=a(x-3)(x+1),把C(2,-3)代入求出a即可;
(2)AC所在直线的解析式为:y=-x-1,根据平行四边形ACQP的面积为12,求出AC边上的高为2
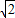
,过点D作DK⊥AC与PQ所在直线相交于点K,求出DK、DN,得到PQ的解析式为y=-x+3或y=-x-5,求出方程组的解,即可得到P
1(3,0),P
2(-2,5),根据ACQP是平行四边形,求出Q的坐标;同法求出以AC为对角线时P、Q的坐标;
(3)设M(t,t
2-2t-3),(-1<t<3),过点M作y轴的平行线,交PQ所在直线于点T,则T(t,-t+3),求出MT=-t
2+t+6,过点M作MS⊥PQ所在直线于点S,求出MS=-
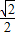
(t-

)
2+
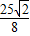
,即可得到答案.
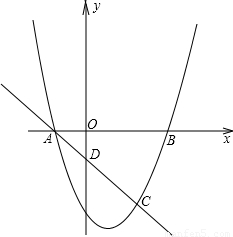
解答:解:(1)∵点A(m-4,0)和C(2m-4,m-6)在直线y=-x+p上
∴
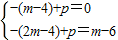
,
解得:
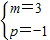
,
∴A(-1,0),B(3,0),C(2,-3),
设抛物线y=ax
2+bx+c=a(x-3)(x+1),
∵C(2,-3),代入得:-3=a(2-3)(2+1),
∴a=1
∴抛物线解析式为:y=x
2-2x-3.
答:抛物线解析式为y=x
2-2x-3.
(2)解:A(-1,0),C(2,-3),由勾股定理得:AC=
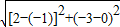
=3
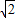
,
AC所在直线的解析式为:y=-x-1,
∠BAC=45°,
∵平行四边形ACQP的面积为12,
∴平行四边形ACQP中AC边上的高为
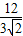
=2
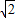
,
过点D作DK⊥AC与PQ所在直线相交于点K,DK=2

,
∴DN=4,
∵四边形ACQP,PQ所在直线在直线ADC的两侧,可能各有一条,
∴根据平移的性质得出直线PQ的解析式为①y=-x+3或②y=-x-5,
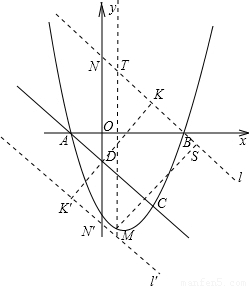
∴由①得:
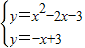
,
解得:
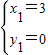
或
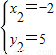
,
由②得:
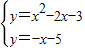
,方程组无解,
即P
1(3,0),P
2(-2,5),
∵ACQP是平行四边形,A(-1,0),C(2,-3),
∴当P(3,0)时,当以AC为边时,Q
1(6,-3),Q
2(0,3),
当P(-2,5)时,当以AC为边时,Q
3(1,2),Q
4(-5,8),
以AC为对角线时,P到AC的距离是12÷2÷(

×3
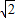
)=2
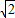
,
过C作CR⊥AC交x轴于R,则AC=CR=3
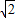
,由勾股定理得:AR=6,
则R的坐标是(5,0)过R作AC的平行线交抛物线于两点,
则此直线的解析式是y=-(x-6)-1=-x+5,
解方程组
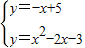
得:
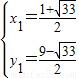
,
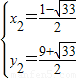
,
即在AC的两旁各有一条直线,但当在AC下方时,直线和抛物线不能相交,
此时P坐标是(
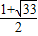
,
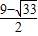
),Q坐标是(
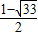
,
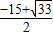
)或P的坐标是(
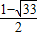
,
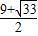
)Q的坐标是(
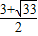
,-
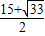
)
答:点P,Q的坐标是P
1(3,0),Q
1(6,-3)或(0,3)
或P
2(-2,5),Q
2(1,2)或(-5,8),或P
3(
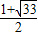
,
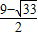
),Q
3(
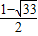
,
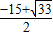
)或P
4(
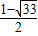
,
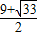
),Q
4(
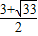
,-
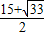
).
(3)解:设M(t,t
2-2t-3),(-1<t<3),
过点M作y轴的平行线,交PQ所在直线于点T,则T(t,-t+3),
MT=(-t+3)-(t
2-2t-3)=-t
2+t+6,
过点M作MS⊥PQ所在直线于点S,
MS=
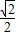
MT=
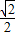
(-t
2+t+6)=-
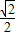
(t-

)
2+
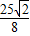
,
则当t=

时,M(

,-
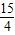
),△PQM中PQ边上高的最大值为
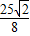
,
∵P
1(3,0),Q
1(6,-3)或P
2(-2,5),Q
2(1,2).
∴当P(3,0),Q(6,-3)时,PQ=
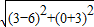
=3
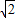
.
当P(-2,5),Q(1,2)时,PQ=
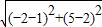
=3
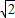
,
∴S
△PQM=

×PQ×
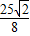
=
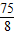
.
答:△PQM的最大面积是
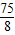
,点M的坐标是(

,-
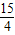
).
点评:本题主要考查对用待定系数法求二次函数的解析式,二次函数的最值,平行四边形的性质,解二元一次方程组等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键,此题是一个综合性比较强的题目,有一定的难度.

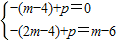 ,求出方程组的解
,求出方程组的解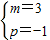 ,得出A、B、C的坐标,设抛物线y=ax2+bx+c=a(x-3)(x+1),把C(2,-3)代入求出a即可;
,得出A、B、C的坐标,设抛物线y=ax2+bx+c=a(x-3)(x+1),把C(2,-3)代入求出a即可;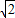 ,过点D作DK⊥AC与PQ所在直线相交于点K,求出DK、DN,得到PQ的解析式为y=-x+3或y=-x-5,求出方程组的解,即可得到P1(3,0),P2(-2,5),根据ACQP是平行四边形,求出Q的坐标;同法求出以AC为对角线时P、Q的坐标;
,过点D作DK⊥AC与PQ所在直线相交于点K,求出DK、DN,得到PQ的解析式为y=-x+3或y=-x-5,求出方程组的解,即可得到P1(3,0),P2(-2,5),根据ACQP是平行四边形,求出Q的坐标;同法求出以AC为对角线时P、Q的坐标;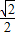 (t-
(t- )2+
)2+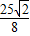 ,即可得到答案.
,即可得到答案.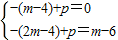 ,
,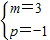 ,
,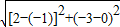 =3
=3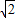 ,
,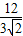 =2
=2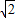 ,
, ,
,
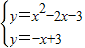 ,
,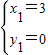 或
或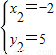 ,
,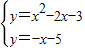 ,方程组无解,
,方程组无解, ×3
×3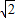 )=2
)=2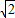 ,
,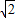 ,由勾股定理得:AR=6,
,由勾股定理得:AR=6,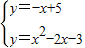 得:
得: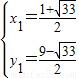 ,
,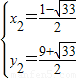 ,
,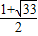 ,
,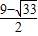 ),Q坐标是(
),Q坐标是(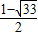 ,
,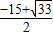 )或P的坐标是(
)或P的坐标是(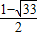 ,
,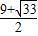 )Q的坐标是(
)Q的坐标是(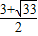 ,-
,-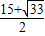 )
)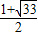 ,
,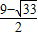 ),Q3(
),Q3(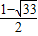 ,
,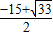 )或P4(
)或P4(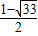 ,
,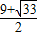 ),Q4(
),Q4(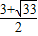 ,-
,-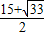 ).
).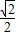 MT=
MT=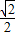 (-t2+t+6)=-
(-t2+t+6)=-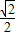 (t-
(t- )2+
)2+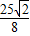 ,
, 时,M(
时,M( ,-
,-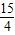 ),△PQM中PQ边上高的最大值为
),△PQM中PQ边上高的最大值为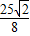 ,
,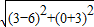 =3
=3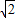 .
.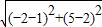 =3
=3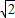 ,
, ×PQ×
×PQ×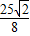 =
=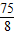 .
.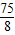 ,点M的坐标是(
,点M的坐标是( ,-
,-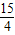 ).
).

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案

 (2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.