
 )以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).
)以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).
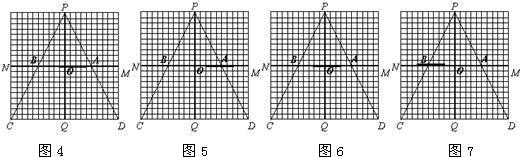
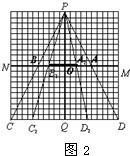
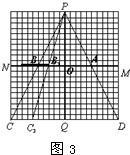
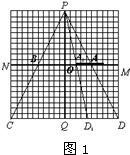 解:(1)在P视点看不见的列车后的区域就是盲区,也就是过P和列车的两端的射线交CD于两点,这两点和列车两端构成的梯形就是所指的盲区.如图1的梯形AA1D1D,图2的梯形A2B2C2D2,图3的梯形B3BCC3.
解:(1)在P视点看不见的列车后的区域就是盲区,也就是过P和列车的两端的射线交CD于两点,这两点和列车两端构成的梯形就是所指的盲区.如图1的梯形AA1D1D,图2的梯形A2B2C2D2,图3的梯形B3BCC3.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源:第3章《圆》中考题集(84):3.5 平行投影和中心投影(解析版) 题型:解答题
 )以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).
)以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).

查看答案和解析>>
科目:初中数学 来源:2012年浙江省杭州市中考数学模拟试卷(四)(解析版) 题型:解答题
 )以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).
)以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).

查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《投影与视图》(02)(解析版) 题型:解答题
 )以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).
)以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).

查看答案和解析>>
科目:初中数学 来源:2005年河北省中考数学试卷(课标卷)(解析版) 题型:解答题
 )以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).
)以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com