
【题目】如图,两个反比例函数y1= ![]() (其中k1>0)和y2=
(其中k1>0)和y2= ![]() 在第一象限内的图象依次是C1和C2 , 点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( )
在第一象限内的图象依次是C1和C2 , 点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( ) 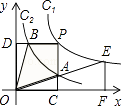
A.![]() ﹕1
﹕1
B.2﹕ ![]()
C.2﹕1
D.29﹕14
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】某电视台组织知识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录了5个参赛者的得分情况.
参赛者 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 18 | 2 | 88 |
D | 14 | 6 | 64 |
E | 10 | 10 | 40 |
(1)参赛者F得76分,他答对了几道题?
(2)参赛者G说他得80分,你认为可能吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中直线y=x+2与反比例函数 y=﹣ ![]() 的图象有唯一公共点,若直线y=x+m与反比例函数y=﹣
的图象有唯一公共点,若直线y=x+m与反比例函数y=﹣ ![]() 的图象有2个公共点,则m的取值范围是( )
的图象有2个公共点,则m的取值范围是( ) 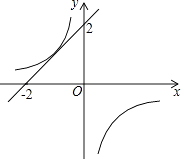
A.m>2
B.﹣2<m<2
C.m<﹣2
D.m>2或m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市第一次用4600元购进甲、乙两种商品,其中甲商品件数的2倍比乙商品件数的3倍少40件,甲、乙两种商品的进价和售价如下表(利润=售价﹣进价):
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 28 | 40 |
(1)该超市第一次购进甲、乙两种商品的件数分别是多少?
(2)该超市将第一次购进的甲、乙两种商品全部卖出后一共可获得多少利润?
(3)该超市第二次以同样的进价又购进甲、乙两种商品.其中甲商品件数是第一次的2倍,乙商品的件数不变.甲商品按原价销售,乙商品打折销售.第二次甲、乙两种商品销售完以后获得的利润比第一次获得的利润多280元,则第二次乙商品是按原价打几折销售的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上.
的图象上.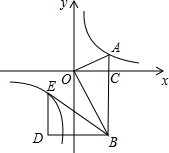
(1)求反比例函数y= ![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP= ![]() S△AOB , 求点P的坐标;
S△AOB , 求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
归纳证明:如图③,点BC在∠MAN的边AM、AN上,点EF在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC, ∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .(12分)




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E. 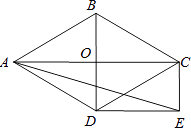
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2 ![]() 时,求sin∠AED的值.
时,求sin∠AED的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com