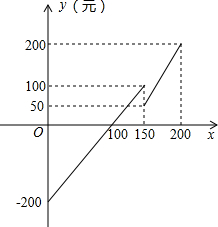
解:(1)当0≤x≤150时,设线段解析式为y=ax+b,
把(0,-200),(150,100)代入,
得
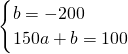
,
解得
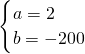
,
所以,y=2x-200,
当150<x≤200时,设线段解析式为y=mx+n,
把(150,50),(200,200)代入,
得
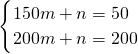
,
解得
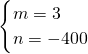
,
所以,y=3x-400;
(2)由y=2x-200,令y=0得x=100,
所以,当售出的票数100张时,此放影厅不赔不赚,
当售出的票数满足0≤x<100时,此放影厅要赔本,
当售出的票数x>100时,此放影厅能赚钱;
(3)把y=100代入y=3x-400中,
得3x-400=100,
解得x=166

,
∴当售出的票数大于166

小于等于200且为整数时,所获得的利润比x=150时多.
分析:(1)根据0≤x≤150和150<x≤200,分段设一次函数解析式,利用待定系数法求一次函数解析式;
(2)当0≤x≤150时,一次函数图象与x轴相交,根据交点坐标,可求不赔不赚,赔本,赚钱,三种情况的x取值范围;
(3)x=150时,y=100,把y=100代入150<x≤200的函数式,求x的值,再求利润比x=150多时,x的取值范围.
点评:本题考查了一次函数的应用.主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题,具备在直角坐标系中的读图能力.注意自变量的取值范围不能遗漏.

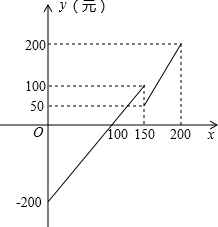 中保险部门规定:超过150人时,要缴纳公安消防保险费50元.试根据关系图,回答下利问题;
中保险部门规定:超过150人时,要缴纳公安消防保险费50元.试根据关系图,回答下利问题;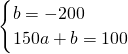 ,
,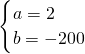 ,
,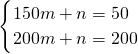 ,
,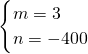 ,
, ,
, 小于等于200且为整数时,所获得的利润比x=150时多.
小于等于200且为整数时,所获得的利润比x=150时多.

 中保险部门规定:超过150人时,要缴纳公安消防保险费50元.试根据关系图,回答下利问题;
中保险部门规定:超过150人时,要缴纳公安消防保险费50元.试根据关系图,回答下利问题;