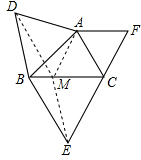
(1)解:DE=EF,DF=EF,∠D=∠E=∠F,A、B、C分别为DF、DE、EF的中点.
(2)证明:过A作AM∥FC交BC于M,连接DM、EM,
∵∠ACB=60°,∠CAF=60°,
∴∠ACB=∠CAF,
∴AF∥MC,
∴四边形AMCF是平行四边形,
又∵FA=FC,
∴四边形AMCF是菱形,
∴AC=CM=AM,且∠MAC=60°,
∵在△BAC与△EMC中,
CA=CM,∠ACB=∠MCE,CB=CE,
∴△BAC≌△EMC,
∵∠DAM=∠DAB+∠BAM=60°+∠BAM
∠BAC=∠MAC+∠BAM=60°+∠BAM
∴∠BAC=∠DAM
在△ABC和△ADM中
AB=AD,∠BAC=∠DAM,AC=AM
∴△ABC≌△ADM(SAS)
故△ABC≌△MEC≌△ADM,
在CB上截取CM,使CM=CA,
再连接AM、DM、EM (辅助线这样做△AMC就是等边三角形了,后边证明更简便)
易证△AMC为等边三角形,
在△ABC与△MEC中,
CA=CM,∠ACB=∠MCE,CB=CE,
∴△ABC≌△MEC(SAS),
∴AB=ME,∠ABC=∠MEC,
又∵DB=AB,
∴DB=ME,
∵∠DBC=∠DBA+∠ABC=60°+∠ABC,
∠BME=∠BCE+∠MEC=60°+∠MEC,
∴∠DBC=∠BME,
∴DB∥ME,
即得到DB与ME平行且相等,故四边形DBEM是平行四边形,
∴四边形DBEM是平行四边形,
∴S
△BDM+S
△DAM+S
△MAC=S
△BEM+S
△EMC+S
△ACF,
即S
△ABC+S
△ABD=S
△BCE+S
△ACF.
分析:(1)由等边三角形的性质可写出结论.
(2)要证明以上结论,需创造一些条件,首先可从△ABC中分出一部分使得与△ACF的面积相等,则过A作AM∥FC交BC于M,连接DM、EM,就可创造出这样的条件,然后再证其它的面积也相等即可.
点评:本题主要考查等边三角形的性质及平行四边的判定和全等三角形的判定,难度很大,有利于培养同学们钻研和探索问题的精神.

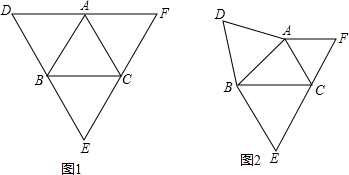 已知△ABC,分别以AB、BC、CA为边向形外作等边三角形ABD、等边三角形BCE、等边三角形ACF.
已知△ABC,分别以AB、BC、CA为边向形外作等边三角形ABD、等边三角形BCE、等边三角形ACF. (1)解:DE=EF,DF=EF,∠D=∠E=∠F,A、B、C分别为DF、DE、EF的中点.
(1)解:DE=EF,DF=EF,∠D=∠E=∠F,A、B、C分别为DF、DE、EF的中点.






