
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 轴正半轴上一点,以
轴正半轴上一点,以![]() 为边作等腰直角三角形
为边作等腰直角三角形![]() ,使
,使![]() ,点
,点![]() 在第一象限。若点
在第一象限。若点![]() 在函数
在函数![]() 的图象上,则
的图象上,则![]() 的面积为( )
的面积为( )
A. ![]() .B.
.B. ![]() .C.
.C. ![]() .D.
.D. ![]() .
.
【答案】C
【解析】
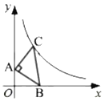
设点B的横坐标为x,过C作x轴,y轴的垂线,易证△OAB≌△DCA,可得CD=OA=1,AD=OB=x,因为点C在y=![]() 图象上,可得矩形ODCE的面积为3,列方程即可得出x的值,然后根据勾股定理求出AB的长,即可得出△ABC的面积.
图象上,可得矩形ODCE的面积为3,列方程即可得出x的值,然后根据勾股定理求出AB的长,即可得出△ABC的面积.
解:设点B的横坐标为x,过C作CE⊥x轴于点E,CD⊥y轴于点D,
∵∠DCA+∠DAC=90°,∠DAC+∠OAB=90°,
∴∠DCA=∠OAB,
在△OAB与△DCA中,
 ,
,
∴△OAB≌△DCA(AAS),
∴CD=OA=1,AD=OB=x,
∴OD=1+x,
∵点C在y=![]() 图象上,
图象上,
∴矩形ODCE的面积为3,
即1×(1+x)=3,
x=2,
∴AC=AB=![]() =
=![]() ,
,
∴S△ABC=![]() ×AB×AC=
×AB×AC=![]() .
.
故选:C.



科目:初中数学 来源: 题型:
【题目】如图,△ABC与 △ADE中,∠ACB=∠AED=90°,连接BD、CE,∠EAC=∠DAB.
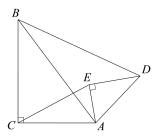
(1)求证:△ABC ∽△ADE;
(2)求证:△BAD ∽△CAE;
(3)已知BC=4,AC=3,AE=![]() .将△AED绕点A旋转,当点E落在线段CD上时,求 BD的长.
.将△AED绕点A旋转,当点E落在线段CD上时,求 BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
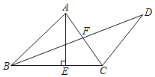
【题目】如图,△ABC中,AE⊥BC于E,点D在∠ABC的平分线上,AC与BD交于F,连CD,∠ACD+2∠ACB=180°,AB=2EC,BD=2![]() ,BE=3,则AF=______.
,BE=3,则AF=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
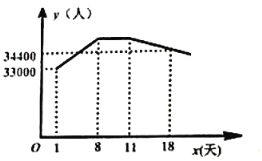
【题目】某市植物园于2019年3月-5月举办花展,按照往年的规律推算,自4月下旬起游客量每天增加![]() 人,游客量预计将在5月1日达到高峰,并持续到5月4日,随后游客量每天有所减少.已知4月24日为第一天起,每天的游客量
人,游客量预计将在5月1日达到高峰,并持续到5月4日,随后游客量每天有所减少.已知4月24日为第一天起,每天的游客量![]() (人)与时间
(人)与时间![]() (天)的函数图像如图所示,结合图像提供的信息,解答下列问题:
(天)的函数图像如图所示,结合图像提供的信息,解答下列问题:
![]() 已知该植物园门票
已知该植物园门票![]() 元/张,若每位游客在园内每天平均消费
元/张,若每位游客在园内每天平均消费![]() 元,试求5月1日-5月4日,所有游客消费总额为多少元?
元,试求5月1日-5月4日,所有游客消费总额为多少元?
![]() 当
当![]() 时,求
时,求![]() 关于
关于![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
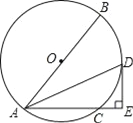
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题提出)
如图①,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.
的取值范围.
(1)(问题解决)
解决此问题可以用如下方法:延长![]() 到点
到点![]() 使
使![]() ,再连接
,再连接![]() (或将
(或将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ),把
),把![]() 、
、![]() 、
、![]() 集中在
集中在![]() 中,利用三角形三边的关系即可判断,由此得出中线
中,利用三角形三边的关系即可判断,由此得出中线![]() 的取值范围.
的取值范围.
(2)(应用)
如图②,在![]() 中,
中,![]() 为
为![]() 的中点,已知
的中点,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
(3)(拓展)
如图③,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,过点
上,过点![]() 作
作![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() 。已知
。已知![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)(1)观察下列算式,并完成填空:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
……
![]() .(
.(![]() 是正整数)
是正整数)
(2)某市一广场用正六边形、正方形和正三角形地板砖铺设图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖,从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.
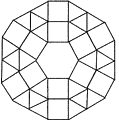
①第3层中分别含有______块正方形和______块正三角形地板砖;
②第![]() 层中含有______块正三角形地板砖(用含
层中含有______块正三角形地板砖(用含![]() 的代数式表示).
的代数式表示).
(应用)
该市打算在一个新建广场中央,也采用这个样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
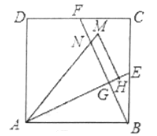
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() ,交点为
,交点为![]() . 若正方形的边长为
. 若正方形的边长为![]() .
.
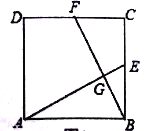
(1)求证:![]() ;
;
(2)将![]() 沿
沿![]() 对折,得到
对折,得到![]() (如图),延长
(如图),延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求
,求![]() 的长;
的长;
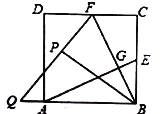
(3)将![]() 绕点
绕点![]() 逆时针方向旋转,使边
逆时针方向旋转,使边![]() 正好落在
正好落在![]() 上,得到
上,得到![]() (如图),若
(如图),若![]() 和
和![]() 相交于点
相交于点![]() ,求四边形
,求四边形![]() 面积.
面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
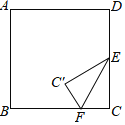
【题目】如图,正方形ABCD的边长是2,点E是CD边的中点,点F是边BC上不与点B,C重合的一个动点,把∠C沿直线EF折叠,使点C落在点C′处.当△ADC′为等腰三角形时,FC的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com