解:问题1:对角线PQ与DC不可能相等。理由如下:
∵四边形PCQD是平行四边形,若对角线PQ、DC相等,则四边形PCQD是矩形,
∴∠DPC=90°。
∵AD=1,AB=2,BC=3,∴DC=2
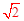
。
设PB=x,则AP=2-x,
在Rt△DPC中,PD
2+PC
2=DC
2,即x
2+3
2+(2-x)
2+1
2=8,化简得x
2-2x+3=0,
∵△=(-2)2-4×1×3=-8<0,∴方程无解。
∴不存在PB=x,使∠DPC=90°。∴对角线PQ与DC不可能相等。
问题2:存在。理由如下:
如图2,在平行四边形PCQD中,设对角线PQ与DC相交于点G,
则G是DC的中点。过点Q作QH⊥BC,交BC的延长线于H。
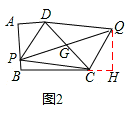
∵AD∥BC,∴∠ADC=∠DCH,即∠ADP+∠PDG=∠DCQ+∠QCH。
∵PD∥CQ,∴∠PDC=∠DCQ。∴∠ADP=∠QCH。
又∵PD=CQ,∴Rt△ADP≌Rt△HCQ(AAS)。∴AD=HC。
∵AD=1,BC=3,∴BH=4,
∴当PQ⊥AB时,PQ的长最小,即为4。
问题3:存在。理由如下:
如图3,设PQ与DC相交于点G,
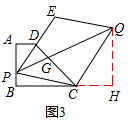
∵PE∥CQ,PD=DE,∴
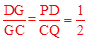
。
∴G是DC上一定点。
作QH⊥BC,交BC的延长线于H,
同理可证∠ADP=∠QCH,∴Rt△ADP∽Rt△HCQ。∴
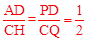
。
∵AD=1,∴CH=2。∴BH=BG+CH=3+2=5。
∴当PQ⊥AB时,PQ的长最小,即为5。
问题4:如图3,设PQ与AB相交于点G,
∵PE∥BQ,AE=nPA,∴
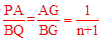
。
∴G是DC上一定点。
作QH∥PE,交CB的延长线于H,过点C作CK⊥CD,交QH的延长线于K。
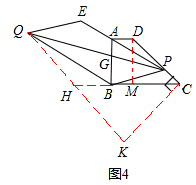
∵AD∥BC,AB⊥BC,
∴∠D=∠QHC,∠DAP+∠PAG=∠QBH+∠QBG=90°
∠PAG=∠QBG,
∴∠QBH=∠PAD。∴△ADP∽△BHQ,∴
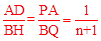
,
∵AD=1,∴BH=n+1。∴CH=BH+BC=3+n+1=n+4。
过点D作DM⊥BC于M,则四边形ABND是矩形。
∴BM=AD=1,DM=AB=2。∴CM=BC-BM=3-1=2=DM。
∴∠DCM=45°。∴∠KCH=45°。
∴CK=CH•cos45°=
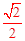
(n+4),
∴当PQ⊥CD时,PQ的长最小,最小值为
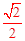
(n+4)。


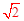 。
。

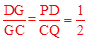 。
。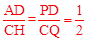 。
。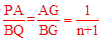 。
。
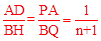 ,
,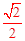 (n+4),
(n+4),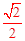 (n+4)。
(n+4)。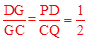 ,易证得Rt△ADP∽Rt△HCQ,继而求得BH的长,即可求得答案。
,易证得Rt△ADP∽Rt△HCQ,继而求得BH的长,即可求得答案。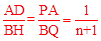 与△ADP∽△BHQ,又由∠DCB=45°,可得△CKH是等腰直角三角形,继而可求得CK的值,即可求得答案。
与△ADP∽△BHQ,又由∠DCB=45°,可得△CKH是等腰直角三角形,继而可求得CK的值,即可求得答案。

 考前必练系列答案
考前必练系列答案


 ,BE=2
,BE=2 .求CD的长和四边形ABCD的面积.
.求CD的长和四边形ABCD的面积.