B
分析:先画图,由AB是⊙O
1和⊙O
2的外公切线,则∠O
1AB=∠O
2BA=90°,再由O
1A=O
1M,O
2B=O
2M,得∠O
1AM=∠O
1MA,∠O
2BM=∠O
2MB,则∠BAM+∠AMO
1=90°,∠ABM+∠BMO
2=90°,则∠AMB=∠BMO
2+∠AMO
1=90°,再由勾股定理求出AB边上的高.
解答:

解:如图,
∵AB是⊙O
1和⊙O
2的外公切线,∴∠O
1AB=∠O
2BA=90°,
∵O
1A=O
1M,O
2B=O
2M,∴∠O
1AM=∠O
1MA,∠O
2BM=∠O
2MB,
∴∠BAM+∠AMO
1=90°,∠ABM+∠BMO
2=90°,
∴∠AMB=∠BMO
2+∠AMO
1=90°,
∴AM⊥BM,
∵MA=4cm,MB=3cm,
∴由勾股定理得,AB=5cm,
由三角形的面积公式,M到AB的距离是

=

cm,
故选B.
点评:本题考查了本题考查的是切线长定理、勾股定理,切线长定理图提供了很多等线段,分析图形时关键是要仔细探索,找出图形的各对相等切线长.

 cm
cm cm
cm cm
cm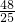 cm
cm 解:如图,
解:如图, =
= cm,
cm,

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案