练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知抛物线与x轴相交于两点A(1，0)，B(-3，0)，与y轴相交于点C(0，3)．
    (1)求此抛物线的函数表达式；
    (2)如果点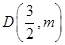是抛物线上的一点，求△ABD的面积．

    （1）；（2）.

    解析试题分析：（1）设抛物线的解析式为. 将A、B两点坐标代入抛物线的解析式中，即可求出待定系数的值，从而确定该二次函数的解析式；
    （2）将D点横坐标代入抛物线的解析式中，即可求出m的值；以AB为底，D点纵坐标的绝对值为高，即可求出△ABD的面积．
    试题解析：
    解：(1)∵抛物线与y轴相交于点C(0，3),
    ∴设抛物线的解析式为.
    ∵抛物线与x轴相交于两点，
    ∴ 解得： 
    ∴抛物线的函数表达式为：.
    （2）∵点是抛物线上一点，
    ∴.
    ∴ .
    考点：二次函数综合题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    在某市开展的环境创优活动中，某居民小区要在一块靠墙（墙长15米）的空地上修建一个矩形花园ABCD，花园的一边靠墙，另三边用总长为40m的栅栏围成，若设花园与墙平行的一边长为x(m)，花园的面积为y(m2)。
    （1）求y与x之间的函数关系式，并写出自变量x的取值范围；
    （2）满足条件的花园面积能达到200m2吗？若能，求出此时x的值，若不能，说明理由：
    （3）根据(1)中求得的函数关系式，判断当x取何值时，花园的面积最大？最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知抛物线与轴相交于，两点（点在点的左侧），与轴相交于点．

    （1）点的坐标为        ，点的坐标为        ；
    （2）在轴的正半轴上是否存在点，使以点，，为顶点的三角形与相似？若存在，求出点的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    二次函数y=x2+bx+c的图象经过点（4,3）,（3,0）．
    （1）b=        ,c=         ；
    （2）选取适当的数据填写下表,并在右图的直角坐标系中画出该函数的图像；

    x
    		…
    		 
    		 
    		 
    		 
    		 
    		…
    y
    		…
    		 
    		 
    		 
    		 
    		 
    		…
     
    （3）若将此图象沿x轴向左平移3个单位,直接写出平移后图象所对应的函数关系式           .

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知抛物线经过（0,-1）,（3,2）两点．求它的解析式及顶点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，在平面直角坐标系xOy中，将抛物线C1：y＝x2＋3先向右平移1个单位，再向下平移7个单位得到抛物线C2。C2的图象与x轴交于A、B两点（点A在点B的左侧）。

    （1）求抛物线C2的解析式；
    （2）若抛物线C2的对称轴与x轴交于点C，与抛物线C2交于点D，与抛物线C1交于点E，连结AD、DB、BE、EA，请证明四边形ADBE是菱形，并计算它的面积；
    （3）若点F为对称轴DE上任意一点，在抛物线C2上是否存在这样的点G，使以O、B、F、G四点为顶点的四边形是平行四边形，如果存在，请求出点G的坐标，如果不存在，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知二次函数y1=ax2＋bx－3的图象经过点A（2，-3），B（-1，0），与y轴交于点C，与x轴另一交点交于点D.

    （1）求二次函数的解析式；
    （2）求点C、点D的坐标；
    （3）若一条直线y2,经过C、D两点，请直接写出y1＞y2时，的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    有两个直角三角形，在△ABC中，∠ACB=90°，AC=3，BC=6，在△DEF中，∠FDE=90°，DE=DF=4。将这两个直角三角形按图1所示位置摆放，其中直角边在同一直线上，且点与点重合。现固定，将以每秒1个单位长度的速度在上向右平移，当点与点重合时运动停止。设平移时间为秒。

    （1）当为       秒时，边恰好经过点；当为       秒时，运动停止；
    （2）在平移过程中，设与重叠部分的面积为，请直接写出与的函数关系式，并写出的取值范围；
    （3）当停止运动后，如图2，为线段上一点，若一动点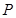从点出发，先沿方向运动，到达点后再沿斜坡方向运动到达点，若该动点在线段上运动的速度是它在斜坡上运动速度的2倍，试确定斜坡的坡度，使得该动点从点运动到点所用的时间最短。（要求，简述确定点位置的方法，但不要求证明。）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    在平面直角坐标系xOy中，一块含60°角的三角板作如图摆放，斜边AB在x轴上，直角顶点C在y轴正半轴上，已知点A（-1，0）．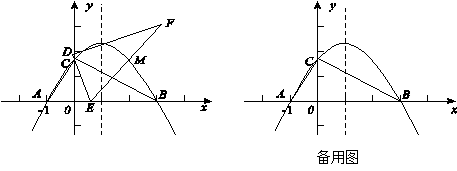

    （1）请直接写出点B，C的坐标：B（  ，  ），C（  ，  ）；
    （2）求经过A，B，C三点的抛物线解析式；
    （3）现有与上述三角板完全一样的三角板DEF（其中∠EDF=90°，∠DEF=60°），把顶点E放在线段AB上（点E是不与A，B两点重合的动点），并使ED所在直线经过点C．此时，EF所在直线与（2）中的抛物线交于第一象限的点M．当AE=2时，抛物线的对称轴上是否存在点P使△PEM是等腰三角形，若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案