
【题目】如图,△ABD和△ACE分别是等边三角形,AB≠AC,下列结论中正确有( )个.

⑴DC=BE,⑵∠BOD=60°,⑶∠BDO=∠CEO,⑷AO平分∠DOE,⑸AO平分∠BAC
A. 2 B. 3 C. 4 D. 5
【答案】B
【解析】
根据等边三角形的性质推出AD=AB,AE=AC,∠ADB=∠ABD=60°,∠DAB=∠EAC=60°,求出∠DAC=∠BAE,根据SAS证△DAC≌△BAE,推出BE=DC,∠ADC=∠ABE,根据三角形的内角和定理求出∠BOD=180°-∠ODB-∠DBA-∠ABE=60°,根据等边三角形性质得出∠ADB=∠AEC=60°,但∠ADC≠∠AEB,过点A作AF⊥DC,AH⊥BE,根据三角形全等得AF=AH,则点A 到角两边距离相等,故点A在角角平分线上,根据以上推出的结论即可得出答案.
∵△ABD与△AEC都是等边三角形,
∴AD=AB,AE=AC,∠ADB=∠ABD=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中
 ,
,
∴△DAC≌△BAE(SAS),
∴BE=DC,∠ADC=∠ABE,
∵∠BOD=180°∠ODB∠DBA∠ABE=180°∠ODB60°∠ADC=120°(∠ODB+∠ADC)=120°60°=60°
∴∠BOD=60°,
∴①正确;②正确;
∵△ABD与△AEC都是等边三角形,
∴∠ADB=∠AEC=60°,但根据已知不能推出∠ADC=∠AEB,
∴说∠BDO=∠CEO错误,∴③错误;
过点A作AF⊥DC,AH⊥BE,分别交DC与BE与点F、H.
∵△DAC≌△BAE,
∴AF=AH,
则点A在∠DOE的角平分线上,
∴OA平分∠DOE,∴④正确;
根据已知条件不能证明OA平分∠BAC,
∴⑤错误.
故答案选:B.


科目:初中数学 来源: 题型:
【题目】如图是放在地面上的一个长方体盒子,其中AB=9cm,BC=6cm,BF=5cm,点M在棱AB上,且AM=3cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为( )

A. 10cm B. ![]() C.
C. ![]() D. 9cm
D. 9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=150°.第一步:在△ABC上方确定一点A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如图1.第二步:在△A1BC上方确定一点A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如图2.照此下去,至多能进行( )步.
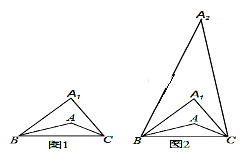
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,求证:AD=DC+AB,
(2)如图②,在四边形ABCD中,AB∥DC,F是DC延长线上一点,连接AF,E是BC的中点,若AE是∠BAF的平分线,求证:AB=AF+CF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. 
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如∠MON=30°、OP=6,点A、B分别在OM、ON上;(1)请在图中画出周长最小的△PAB(保留画图痕迹);(2)请求出(1)中△PAB的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y= ![]() 的图象如图,以下结论:
的图象如图,以下结论:
①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
其中正确的个数是( )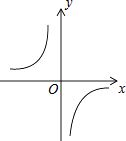
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,格点△ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识.

(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的三角形A1B1C1;
(3)判断△ABC的形状,并求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,BO,CO分别是∠ABC和∠ACB的平分线,过O点的直线分别交AB、AC于点D、E,且DE∥BC.若AB=6 cm,AC=8 cm,则△ADE的周长为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com