B
分析:设从2007年开始经过n年可以将全县所有的坡荒地全部种上树木,根据表格知道每年又以比上一年多植400亩,所以d=400,a=1000,根据阅读材料可以得到方程25000=1400n+

×400,解方程即可求出经过.
解答:从表中可知,2007年植树1000公顷,以后每年均比上一年多植树400公顷.
2007年实有坡荒地25200公顷.
种树1400公顷后,实有坡荒地只减少丁25200-24000=1200(公顷),
因此,每年新产生的坡荒地为200公顷,即树木实际存活1200公顷.
设从2008年起(2008年算第1年),n年全县的坡荒地全部植树,
有1400n+

×400-200n≥25200.
即:n
2+5n≥126.
估算:当n=8时,82+5×8=104≤126.
当n=9时,92+5×9=126.
故到2016年,可将全县所有的坡荒地全部种上树木.
故选B.
点评:这是一道新颖独特的阅读题,它的基本形式可归纳为:“阅读--理解--应用”,解题时应抓住三点:(1)读:读懂材料,读懂表格;(2)用:把阅读材料提供的结论正确地套用于解题中;(3)活:指解题时的计算,对n2+5n≥126这样的不等式,用估算法求年数n.

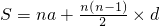 来计算它们的和(公式中的n表示数的个数,a表示第一个数的值,d表示这个相差的定值).
来计算它们的和(公式中的n表示数的个数,a表示第一个数的值,d表示这个相差的定值). 
 ×400,解方程即可求出经过.
×400,解方程即可求出经过. ×400-200n≥25200.
×400-200n≥25200.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案