
【题目】在△ABC中,以线段AB为边作△ABD,使得AD=BD,连接DC,再以DC为边作△CDE,使得DC=DE,∠CDE=∠ADB=a。
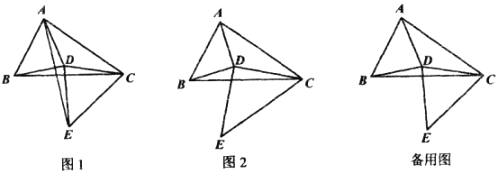
(1)如图1,连结AE,求证:AE=BC;
(2)如图2,BC=4时,将线段CB沿着射线CE的方向平移,得到线段EF,连接BF,AF。
①若![]() =90°,依题意补全图2,求线段AF的长;
=90°,依题意补全图2,求线段AF的长;
②请直接写出线段AF的长(用含![]() 的式子表示)。
的式子表示)。
【答案】(1)证明见解析;
(2)补全图形见解析,AF的长为![]()
(3)AF的长为8sin![]()
【解析】分析(1)由∠ADB=∠CDE,可得∠ADE=∠BDC,据SAS得到△ADE≌△BDC,从而得证.(2)①设DE与BC相交于点H,连接 AE,交BC于点G,根据SAS推出△ADE≌△BDC,根据全等三角形的性质得出AE=BC,∠AED=∠BCD.求出∠AFE=45°,解直角三角形求出即可;②过E作EM⊥AF于M,根据等腰三角形的性质得出∠AEM=∠FEM=![]() ,AM=FM,解直角三角形求出FM即可.
,AM=FM,解直角三角形求出FM即可.
本题解析: 分析:(1)(1)∵∠ADB=∠CDE,
∴∠ADB+∠BDE=∠CDE+∠BDE,∴∠ADE=∠BDC,
在△ADE与△BDC中,
∵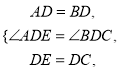
∴△ADE≌△BDC。∴AE=BC
(2)①补全图形。设DE与BC相交于点H,连接AE,交BC于点G,如图:
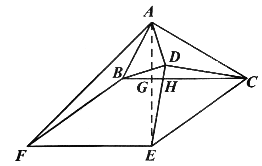
由(1)得△ADE≌△BDC。∴∠AED=∠BCD。
∵DE与BC相交于点H,∴∠GHE=∠DHC。
∴∠EGH=∠EDC=90°。
∵线段CB沿着射线CE的方向平移,得到线段EF,
∴EF=CB=4,EF∥CB。∴AE=EF。
∵CB∥EF,∴∠AEF=∠EGH=90°。
∵AE=EF,∠AEF=90°,∴∠AFE=45°。
∴AF=![]() 。
。
②如图2,
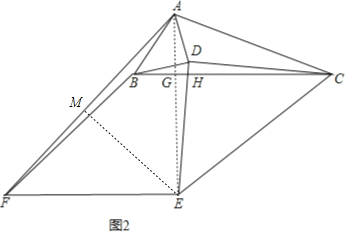
过E作EM⊥AF于M,∵由①知:AE=EF=BC,
∴∠AEM=∠FEM=![]() ,AM=FM,∴AF=2FM=EF×sin
,AM=FM,∴AF=2FM=EF×sin![]() =8sin
=8sin![]() .
.


科目:初中数学 来源: 题型:
【题目】下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm
B.7cm,4cm,2cm
C.3cm,4cm,8cm
D.3cm,3cm,4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:直线l与直线l外一点A。求作:过点A作直线l的平行线。

小明的作法如下:
如图,

①在直线l上任取两点B,C;
②以点A为圆心,线段BC的长为半径作圆弧;以点C为圆心,线段AB的长为半径作圆弧;两圆弧(与点A在l同侧)的交点为D;
③过点A,D作直线。所以直线AD即为所求。
老师说:“小明的作法正确。”
该作图的依据是_____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD=![]() 时, 若CD=
时, 若CD=![]() ,求AD长.
,求AD长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com