
分析 (1)根据方程有两个实数根可以得到△≥0,从而求得k的取值范围;
(2)利用根与系数的关系将两根之和和两根之积代入代数式求k的值即可.
解答 解:(1)∵方程有实数根,
∴△=[2(k-1)]2-4k2≥0,
解得k≤$\frac{1}{2}$.
(2)由根与系数关系知:$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2(k-1)}\\{{x}_{1}{x}_{2}={k}^{2}}\end{array}\right.$,
又|x1+x2|=x1x2-6,化简代入得|2(k-1)|=k2-6,
∵k≤$\frac{1}{2}$,
∴2(k-1)<0,
∴-2(k-1)=k2-6,
解得k1=-4,k2=2(舍去)
∴k=-4.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.


科目:初中数学 来源: 题型:解答题
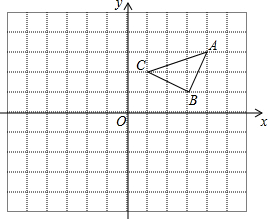 如图,将三角形ABC先向左平移5个单位长度,再向下平移4个单位长度得到三角形A1B1C1.
如图,将三角形ABC先向左平移5个单位长度,再向下平移4个单位长度得到三角形A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
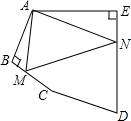 如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为88°.
如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为88°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
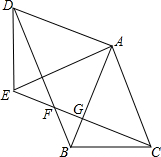 如图,在△ABC中,AB=AC=2,∠BAC=45°,△ABC绕点A顺时针旋转90°后得到△ADE,连接CE、BD、CE交BD于F,交AB于G.
如图,在△ABC中,AB=AC=2,∠BAC=45°,△ABC绕点A顺时针旋转90°后得到△ADE,连接CE、BD、CE交BD于F,交AB于G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com