Question

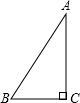
在Rt△ABC，∠C=90°
（1）若a：b=3：4，c=10，求a、b的值．
（2）若b=6，∠A=45°，求a、c长度．

Answer 1

解：（1）∵a：b=3：4，
∴设a=3k，b=4k，（k＞0）
根据勾股定理得，（3k）²+（4k）²=10²，
∴25k²=100，
解得k=2，
∴a=3×2=6，b=4×2=8；

（2）tanA=，cosA=
∵b=6，∠A=45°，
∴=1，=，
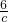
解得a=6，c=6．
分析：（1）根据比例设a=3k，b=4k，利用勾股定理列式求出k的值，然后即可得解；
（2）根据∠A的正切值列式即可求出a的值，∠A的余弦列式即可求出c的值．
点评：本题考查了解直角三角形，主要利用了锐角三角形函数与勾股定理，是基础题，要理清直角三角形中的边角之间的关系．