
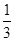 n(n+1)(n��1)ʱ�����ǿ�����������
n(n+1)(n��1)ʱ�����ǿ�����������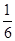 ��
�� 
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2012ѧ���˽̰��п���ѧ��һ�ָ�ϰ������ר��ѵ�� ���ͣ������
��2011�Ĵ��ڽ�������5��12�֣�ͬѧ�ǣ����������о���n��n�����������õ��������������ε������ı���ʽΪ12+22+32+��+n2����nΪ100ʱ��Ӧ��μ��������εľ��������?�������Ǿ�һ����̽�������������⣮���ȣ�ͨ��̽�������Ѿ�֪��0��1+1��2+2��3+��+(n��1)��n= n(n+1)(n��1)ʱ�����ǿ�����������
n(n+1)(n��1)ʱ�����ǿ�����������
(1)�۲첢���룺
12+22=(1+0)��1+(1+1)��2=1+0��1+2+1��2=(1+2)+(0��1+1��2)
12+22+32=(1+0)��1+(1+1)��2+(1+2)��3
=1+0��1+2+1��2+3+2��3
=(1+2+3)+(0��1+1��2+2��3)
12+22+32+42=(1+0)��1+(1+1)��2+(1+2)��3+
=1+0��1+2+1��2+3+2��3+
=(1+2+3+4)+( )
����
(2)���ɽ��ۣ�
12+22+32+��+n2=(1+0)��1+(1+1)��2+(1+2)��3+��+n
=1+0��1+2+1��2+3+2��3+��+n+(nһ1)��n
=( ) +
= +
= ��
��
(3)ʵ��Ӧ�ã�
ͨ������̽�����̣����ǾͿ��������nΪ100ʱ�������������������ε��ܸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012ѧ���˽̰��п���ѧ��һ�ָ�ϰ������ר��ѵ�� ���ͣ������
��2011�Ĵ��ڽ�������5��12�֣�ͬѧ�ǣ����������о���n��n�����������õ��������������ε������ı���ʽΪ12+22+32+��+n2����nΪ100ʱ��Ӧ��μ��������εľ��������?�������Ǿ�һ����̽�������������⣮���ȣ�ͨ��̽�������Ѿ�֪��0��1+1��2+2��3+��+(n��1)��n= n(n+1)(n��1)ʱ�����ǿ�����������
n(n+1)(n��1)ʱ�����ǿ�����������
(1)�۲첢���룺
12+22=(1+0)��1+(1+1)��2=1+0��1+2+1��2=(1+2)+(0��1+1��2)
12+22+32=(1+0)��1+(1+1)��2+(1+2)��3
=1+0��1+2+1��2+3+2��3
=(1+2+3)+(0��1+1��2+2��3)
12+22+32+42=(1+0)��1+(1+1)��2+(1+2)��3+
=1+0��1+2+1��2+3+2��3+
=(1+2+3+4)+( )
����
(2)���ɽ��ۣ�
12+22+32+��+n2=(1+0)��1+(1+1)��2+(1+2)��3+��+n
=1+0��1+2+1��2+3+2��3+��+n+(nһ1)��n
=( ) +
= +
= ��
��
(3)ʵ��Ӧ�ã�
ͨ������̽�����̣����ǾͿ��������nΪ100ʱ�������������������ε��ܸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012ѧ���˽̰��п���ѧ��һ�ָ�ϰ������ר��ѵ�� ���ͣ�ѡ����
��2011�Ĵ��ڽ���3��3�֣�ij������ң���������ĺ����߲���Ϊ0.000 000 94m���ÿ�ѧ��������ʾ������ǣ� ��
A��9.4��10��7 m B��9.4��107m C��9.4��10��8m D��9.4��108m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012ѧ���˽̰��п���ѧ��һ�ָ�ϰ��ʽר��ѵ�� ���ͣ�ѡ����
��2011�Ĵ��ڽ���15��5�֣������ʽ ��ֵΪ0����x��ֵӦΪ
��
��ֵΪ0����x��ֵӦΪ
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com