
 如图,在Rt△ABC中,∠A=30°,点D是斜边AB的中点,点G是Rt△ABC的重心,GE⊥AC于点E.若BC=6cm,则GE=2cm.
如图,在Rt△ABC中,∠A=30°,点D是斜边AB的中点,点G是Rt△ABC的重心,GE⊥AC于点E.若BC=6cm,则GE=2cm. 分析 根据在直角三角形中,30°所对的直角边是斜边的一半得到AB=2BC=12cm,根据直角三角形斜边上的中线是斜边的一半CD=$\frac{1}{2}$AB=6cm,根据重心的性质得到CG=$\frac{2}{3}$CD=4cm,根据30°所对的直角边是斜边的一半得到答案.
解答 解:在Rt△ABC中,∠A=30°,
∴AB=2BC=12cm,
在Rt△ABC中,点D是斜边AB的中点,
∴CD=$\frac{1}{2}$AB=6cm,
∵点G是Rt△ABC的重心,
∴CG=$\frac{2}{3}$CD=4cm,
∵CD=AD,∴∠DCA=∠A=30°,
∴GE=$\frac{1}{2}$CG=2cm,
故答案为:2.
点评 本题考查的是三角形的重心的性质和直角三角形的性质,掌握重心到顶点的距离是它到对边中点的距离的2倍是解题的关键,注意在直角三角形中,30°所对的直角边是斜边的一半、直角三角形斜边上的中线是斜边的一半.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
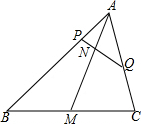 如图,已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.
如图,已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在四边形ABCD中,AB=CD,AD=BC,试判断AB与CD、AD与BC之间有什么样的位置关系,说明理由.除前面的结论外.你还能得到哪些结论?请写出来.
在四边形ABCD中,AB=CD,AD=BC,试判断AB与CD、AD与BC之间有什么样的位置关系,说明理由.除前面的结论外.你还能得到哪些结论?请写出来.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将等腰直角三角形ABC绕点A逆时针旋转30°后得到△AB′C′,B′C′交AB于点D,则∠B′AC=75度,若AC=1,图中阴影部分的面积是=$\frac{2-\sqrt{3}}{2}$.
如图,将等腰直角三角形ABC绕点A逆时针旋转30°后得到△AB′C′,B′C′交AB于点D,则∠B′AC=75度,若AC=1,图中阴影部分的面积是=$\frac{2-\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
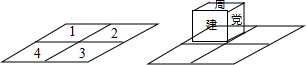 如图,平面上有四个方格,把一个正方体放在1号格上,向右翻转右侧面压在2号格上,再翻向3号格、4号格,再翻回1号格,这样循环翻动下去,如果开始时,正方体的正面、右侧面、后面、左侧面、顶面、底面依次写有“建党九十周年”字样,那么当正方体出发后周字第20次回到顶面时,正方体所在格是1号.
如图,平面上有四个方格,把一个正方体放在1号格上,向右翻转右侧面压在2号格上,再翻向3号格、4号格,再翻回1号格,这样循环翻动下去,如果开始时,正方体的正面、右侧面、后面、左侧面、顶面、底面依次写有“建党九十周年”字样,那么当正方体出发后周字第20次回到顶面时,正方体所在格是1号.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2(y+z)}{x+3(y+z)}$=$\frac{2}{x+3}$ | B. | $\frac{x+y}{{x}^{2}+{y}^{2}}$=$\frac{2}{x+y}$ | ||
| C. | $\frac{(x-y)^{2}}{(y-x)^{2}}$=-1 | D. | $\frac{y-x}{2xy-{x}^{2}-{y}^{2}}$=$\frac{1}{x-y}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com