
 mn,那么当AC、BD所夹的锐角为θ时(如图),四边形ABCD的面积S= .(用含m、n、θ的式子表示)
mn,那么当AC、BD所夹的锐角为θ时(如图),四边形ABCD的面积S= .(用含m、n、θ的式子表示)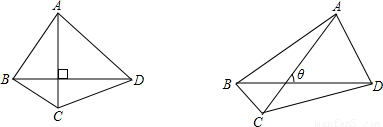
 BD•AE+
BD•AE+ BD•CF=
BD•CF= BD•(AE+CF ),由此也可以求出面积.
BD•(AE+CF ),由此也可以求出面积. m•OC+
m•OC+ m•OA=
m•OA= mn;
mn;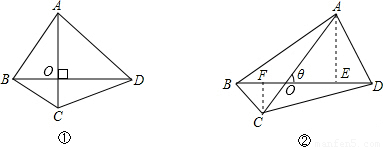
 BD•AE+
BD•AE+ BD•CF
BD•CF BD•(AE+CF)=
BD•(AE+CF)= mnsinθ.
mnsinθ. mnsinθ.
mnsinθ.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源:2008年全国中考数学试题汇编《锐角三角函数》(03)(解析版) 题型:填空题
 mn,那么当AC、BD所夹的锐角为θ时(如图),四边形ABCD的面积S= .(用含m、n、θ的式子表示)
mn,那么当AC、BD所夹的锐角为θ时(如图),四边形ABCD的面积S= .(用含m、n、θ的式子表示)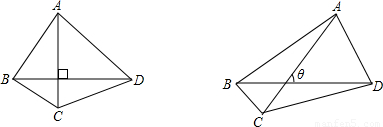
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《四边形》(02)(解析版) 题型:选择题
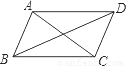
查看答案和解析>>
科目:初中数学 来源:2008年山东省泰安市中考数学试卷(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2008年山东省泰安市中考数学试卷(解析版) 题型:填空题
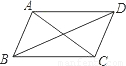
 mn,那么当AC、BD所夹的锐角为θ时(如图),四边形ABCD的面积S= .(用含m、n、θ的式子表示)
mn,那么当AC、BD所夹的锐角为θ时(如图),四边形ABCD的面积S= .(用含m、n、θ的式子表示)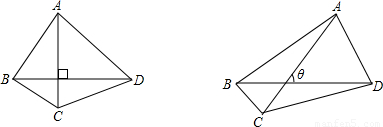
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com