

分析 (1)当E、F分别为BA、AC中点时,EF为三角形ABC中位线,在直角三角形ABC中,利用勾股定理求出BC的长,即可确定出EF的长;
(2)①根据题意利用等式的性质得到一对角相等,再由一对角为45°,利用两对角相等的三角形相似得到三角形BOE与三角形OCF相似,由相似得比例列出y与x间的函数解析式,并求出x的范围即可;
②EF与圆O相切,理由为:由①得出的三角形BOE与三角形COF相似,得比例,把CO换为BO,变形后利用两边对应成比例且夹角相等的三角形相似得到三角形BEO与三角形OEF相似,利用相似三角形对应角相等得到∠BEO=∠FEO,利用角平分线定理得到O到EB、EF的距离相等,而AB与圆O相切,可得出∠OFE=90°,即OF与AC垂直,且OF为半径,即可确定出EF与圆O相切.
解答 解:(1)在△ABC中,AB=AC=2,
∴根据勾股定理得:BC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∵点E,F分别为边BA,AC的中点,
∴EF是△ABC的中位线,
∴EF=$\sqrt{2}$;
(2)在△OEB和△FOC中,
∵∠EOB+∠FOC=135°,∠EOB+∠OEB=135°,
∴∠FOC=∠OEB,
又∵∠B=∠C,
∴△OEB∽△FOC,
∴$\frac{BE}{CO}$=$\frac{BO}{FC}$,
∵BE=x,CF=y,OB=OC=$\sqrt{2}$,
∴$\frac{x}{\sqrt{2}}$=$\frac{\sqrt{2}}{y}$,即y=$\frac{2}{x}$,其中1≤x≤2;
(3)EF与⊙O相切,理由为:
∵△OEB∽△FOC,
∴$\frac{OE}{FO}$=$\frac{BE}{CO}$,
∴$\frac{OE}{FO}$=$\frac{BE}{BO}$,即$\frac{OE}{BE}$=$\frac{FO}{BO}$,
又∵∠B=∠EOF=45°,
∴△BEO∽△OEF,
∴∠BEO=∠OEF,
∴点O到AB和EF的距离相等,
∵AB与⊙O相切,
∴点O到EF的距离等于⊙O的半径,
∴EF与⊙O相切.
点评 此题属于圆综合题,涉及的知识有:相似三角形的判定与性质,勾股定理,三角形中位线定理,以及直线与圆相切的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:选择题
| A. | 9.43×104 | B. | 943×106 | C. | 9.43×106 | D. | 9.43×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,我边防哨所A测得一走私船在A的西北方向B处由南向北正以每小时10海里的速度逃跑,我缉私艇迅速朝A的西偏北60°的方向出发拦截,2小时后终于在B地正北方向M处拦截住,试求缉私船的速度.(结果保留根号)
如图,我边防哨所A测得一走私船在A的西北方向B处由南向北正以每小时10海里的速度逃跑,我缉私艇迅速朝A的西偏北60°的方向出发拦截,2小时后终于在B地正北方向M处拦截住,试求缉私船的速度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
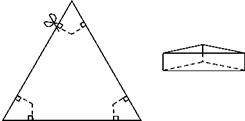 如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为144cm3.
如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为144cm3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
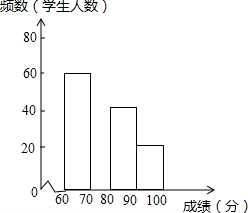 在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:| 成绩 | 频数 | 频率 |
| 60≤x<70 | 60 | 0.30 |
| 70≤x<80 | m | 0.40 |
| 80≤x<90 | 40 | n |
| 90≤x≤100 | 20 | 0.10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com