
分析 根据韦达定理知a+b=4、c+d=5,将t=$\frac{a}{b+c+d}$+$\frac{b}{a+c+d}$+$\frac{c}{a+b+d}$+$\frac{d}{a+b+c}$两边都乘以a+b+c+d,变形后可得t(a+b+c+d)=$\frac{{a}^{2}}{b+c+d}$+a+$\frac{{b}^{2}}{a+c+d}$+b+$\frac{{c}^{2}}{a+b+d}$+c+$\frac{{d}^{2}}{a+b+c}$+d即$\frac{{a}^{2}}{b+c+d}$+$\frac{{b}^{2}}{a+c+d}$+$\frac{{c}^{2}}{a+b+d}$+$\frac{{d}^{2}}{a+b+c}$=t(a+b+c+d)-(a+b+c+d),代入可得答案.
解答 解:根据题意知,a+b=4,c+d=5,
∵t=$\frac{a}{b+c+d}$+$\frac{b}{a+c+d}$+$\frac{c}{a+b+d}$+$\frac{d}{a+b+c}$,
∴t(a+b+c+d)=$\frac{a(a+b+c+d)}{b+c+d}$+$\frac{b(a+b+c+d)}{a+c+d}$+$\frac{c(a+b+c+d)}{a+b+d}$+$\frac{d(a+b+c+d)}{a+b+c}$
=a($\frac{a}{b+c+d}+1$)+b($\frac{b}{a+c+d}+1$)+c($\frac{c}{a+b+d}+1$)+d($\frac{d}{a+b+c}+1$)
=$\frac{{a}^{2}}{b+c+d}$+a+$\frac{{b}^{2}}{a+c+d}$+b+$\frac{{c}^{2}}{a+b+d}$+c+$\frac{{d}^{2}}{a+b+c}$+d,
∴$\frac{{a}^{2}}{b+c+d}$+$\frac{{b}^{2}}{a+c+d}$+$\frac{{c}^{2}}{a+b+d}$+$\frac{{d}^{2}}{a+b+c}$=t(a+b+c+d)-(a+b+c+d)=9t-9.
点评 本题主要考查根与系数的关系,将已知等式两边都乘以a+b+c+d通过变形得到待求代数式是解决此题的关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | ac<bc | B. | a2<b2 | C. | a+1<b+1 | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,?ABCD的周长为20cm,AE⊥BC于点E,AF⊥CD于点F,AE:AF=2:3,∠C=120°,则?ABCD的面积为24cm2.
如图所示,?ABCD的周长为20cm,AE⊥BC于点E,AF⊥CD于点F,AE:AF=2:3,∠C=120°,则?ABCD的面积为24cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
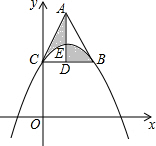 如图,在平面直角坐标系中,点C是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上另一点,且BC∥x轴,以CB为边向上作等边三角形ABC,BC边上的高AD交抛物线于点E,则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$.
如图,在平面直角坐标系中,点C是抛物线y=a(x-3)2+k与y轴的交点,点B是这条抛物线上另一点,且BC∥x轴,以CB为边向上作等边三角形ABC,BC边上的高AD交抛物线于点E,则阴影部分图形的面积为$\frac{9}{2}$$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
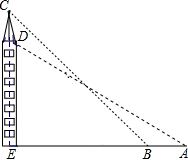 如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )
如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )| A. | 20$\sqrt{3}$ | B. | 20$\sqrt{3}$-8 | C. | 20$\sqrt{3}$-28 | D. | 20$\sqrt{3}$-20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com