练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

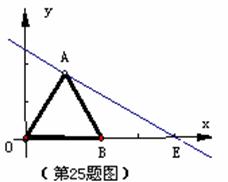
    如图，△OAB是边长为2的等边三角形，过点A的直线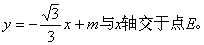

    （1） 求点E的坐标；

    （2） 求过 A、O、E三点的抛物线解析式；

    （3） 若点P是（2）中求出的抛物线AE段上一动点（不与A、E重合），

    设四边形OAPE的面积为S，求S的最大值。


     解：（1）作AF⊥x轴与F

    ∴OF=OAcos60°=1，AF=OFtan60°=

    ∴点A（1，）

    代入直线解析式，得，∴m=

    ∴

    当y=0时，

    得x=4，   ∴点E（4，0）

    （2）设过A、O、E三点抛物线的解析式为

    ∵抛物线过原点

    ∴c=0

                 

    ∴                                    

     ∴

    ∴抛物线的解析式为…

    （3）作PG⊥x轴于G，设

      

     

    当

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


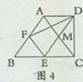
    如图4，在梯形ABCD中，AD∥BC，∠BCD=90°，BC=2AD，F，E分别是AB，BC的中点，则下列结论不一定正确的是（    ）

      A.△ABC是等腰三角形         B.四边形EFAM是菱形

      C.S△BEF=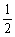S△ACD                       D.DE平分∠CDF

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一项工程要在限期内完成，如果第一组单独做，恰好按规定日期完成；如果第二组单独

       做，需要超过规定日期4天才能完成，如果两组合作3天后，剩下的工程由第二组单独

       做，正好在规定日期内完成，问规定日期是多少天？


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直线l和双曲线y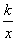＝(k>0)交于A，B两点，P是线段AB上的点(不与A，B重合)，过点A，B，P分别向x轴作垂线，垂足分别是C，D，E，连接OA，OB，OP，设△AOC面积是S1，△BOD面积是S2，△POE面积是S3，则(　)

    A．S1＜S2＜S3 B．S1>S2>S3

    C．S1＝S2>S3 D．S1＝S2<S3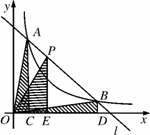

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    为解决停车难的问题，在如图一段长56米的路段开辟停车位，每个车位是长5米、宽2.2米的矩形，矩形的边与路的边缘成45°角，那么这个路段最多可以划出____个

    这样的停车位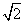．(≈1.4)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    顺次连接四边形四边中点所组成的四边形是菱形，则原四边形为：

       A.平行四边形     B.菱形     C.对角线相等的四边形   D.直角梯形

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在、0.2、、、、中，无理数的个数是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    4的平方根是                                                                （      ）

    A．2                 B．－2                  C．±2                  D．±

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：3xy2·(－5x3y)=_______________.。

    查看答案和解析>>

    同步练习册答案