
分析 先根据分式混合运算的法则把原式进行化简,再根据特殊角的三角函数求出x、y的值,进而可得出x-y与x+y的值,代入代数式进行计算即可.
解答 解:原式=[$\frac{x+y}{(x+y)(x-y)}$-$\frac{x-y}{(x+y)(x-y)}$]•$\frac{(x-y)^{2}}{y}$
=$\frac{2y}{(x+y)(x-y)}$•$\frac{{(x-y)}^{2}}{y}$
=$\frac{2(x-y)}{x+y}$
由x=$\frac{1}{2sin45°-1}$=$\frac{1}{2×\frac{\sqrt{2}}{2}-1}$=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1,y=2sin30°-$\sqrt{2}$=2×$\frac{1}{2}$-$\sqrt{2}$=1-$\sqrt{2}$,
得x-y=2$\sqrt{2}$,x+y=2,
故原式=$\frac{2×2\sqrt{2}}{2}$=2$\sqrt{2}$.
点评 本题考查的是分式的化简求值,分式化简求值时需注意,一般是先化简为最简分式或整式,再代入求值.化简时不能跨度太大,而缺少必要的步骤.


科目:初中数学 来源: 题型:解答题
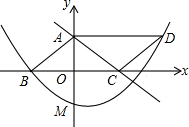 如图,平行四边形ABCD中,D点在抛物线y=$\frac{1}{8}$x2+bx+c上,且OB=OC,AB=5,tan∠ACB=$\frac{3}{4}$,M是抛物线与y轴的交点.
如图,平行四边形ABCD中,D点在抛物线y=$\frac{1}{8}$x2+bx+c上,且OB=OC,AB=5,tan∠ACB=$\frac{3}{4}$,M是抛物线与y轴的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
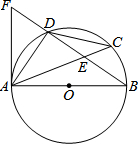 如图,AB是⊙O的直径,D是$\widehat{AC}$的中点,弦AC与弦BD交于点E,点F在BD的延长线上,且DF=DE.
如图,AB是⊙O的直径,D是$\widehat{AC}$的中点,弦AC与弦BD交于点E,点F在BD的延长线上,且DF=DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
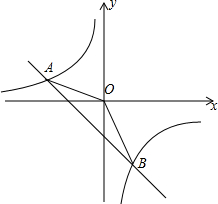 如图,一次函数y=kx-1的图象与反比例函数$y=\frac{m}{x}$的图象相交于A、
如图,一次函数y=kx-1的图象与反比例函数$y=\frac{m}{x}$的图象相交于A、查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
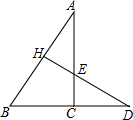 如图所示,DH⊥AB于H,AC⊥BD于C,DH与AC相交于点E,仔细观察图形,回答以下问题:
如图所示,DH⊥AB于H,AC⊥BD于C,DH与AC相交于点E,仔细观察图形,回答以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com