
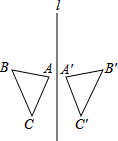
 如图,△ABC关于直线l做了轴反射后得到的像为△A′B′C′,且∠A=78°,∠C′=48°,∠B′=54°,∠C=48°,则∠B的度数为
如图,△ABC关于直线l做了轴反射后得到的像为△A′B′C′,且∠A=78°,∠C′=48°,∠B′=54°,∠C=48°,则∠B的度数为 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
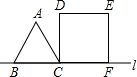 如图,(单位:cm)边长为10cm的等边△ABC以1cm/s的速度沿直线L向边长为10cm的正方形CDEF的方向移动,直到点B与点F重合,△ABC与正方形CDEF重叠部分的面积S关于平移动时间t的函数图象可能是( )
如图,(单位:cm)边长为10cm的等边△ABC以1cm/s的速度沿直线L向边长为10cm的正方形CDEF的方向移动,直到点B与点F重合,△ABC与正方形CDEF重叠部分的面积S关于平移动时间t的函数图象可能是( )A、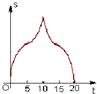 | B、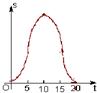 | C、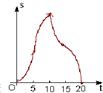 | D、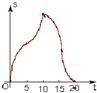 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省江山市中考一模数学试卷(解析版) 题型:解答题
如图1,在等腰梯形ABCD中,AB∥CO,E是AO的中点,过点E作EF∥OC交BC于F,AO=4,OC=6,∠AOC=60°.现把梯形ABCO放置在平面直角坐标系中,使点O与原点重合,OC在x轴正半轴上,点A、B在第一象限内。
(1) 求点E的坐标;
(2) 点P为线段EF上的一个动点,过点P作PM⊥EF交OC于点M,过M作MN∥AO交折线ABC于点N,
连结PN。设PE=x.△PMN的面积为S。
① 求S关于x的函数关系式;
② △PMN的面积是否存在最大值,若不存在,请说明理由。若存在,求出面积的最大值;
(3)另有一直角梯形EDGH(H在EF上,DG落在OC上,∠EDG=90°,且DG=3,HG∥BC)。现在开始操作:固定等腰梯形ABCO,将直角梯形EDGH以每秒1个单位的速度沿OC方向向右移动,直到点D与点C重合时停止(如图2)。设运动时间为t秒,运动后的直角梯形为E′D′G′H′;探究:在运动过程中,等腰梯形ABCO与直角梯形E′D′G′H′重合部分的面积y与时间t的函数关系式。



查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北省黄冈市八年级上学期期中考试数学卷(解析版) 题型:解答题
△ABC在平面直角坐标系中的位置如图所示:
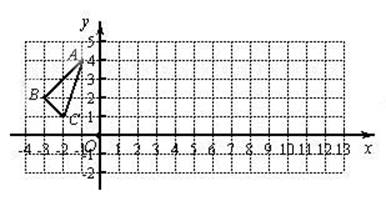
①作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
②将△ABC向右平移8个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
③观察△A1B1C1与△A2B2C2它们是否关于某直成对称?若是,请在图上画出这条对称轴.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年四川省沐川县初三二调考试数学卷(解析版) 题型:解答题
从甲、乙两题中选做一题,如果两题都做,只以甲题计分.
1.甲题:若关于x的一元二次方程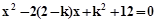 有实数根α、β.求实数k的取值范围;设
有实数根α、β.求实数k的取值范围;设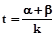 ,求t的最小值.
,求t的最小值.
2.乙题:如图,在△ABC 中,点O是AC边上的一个动点,过点O作直
线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com