练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．已知关于x的方程$\frac{x+a}{2}$-1=3x+4的解是不等式5x+7＞0的一个解，求a的取值范围．

    分析 通过解不等式得出x的取值范围，通过解方程得出a关于x的函数关系式，代入x的取值范围即可得出结论．

    解答 解：解不等式：5x+7＞0，
    得：x＞-$\frac{7}{5}$．
    解方程：$\frac{x+a}{2}$-1=3x+4，
    得：a=5x+10，
    ∵x＞-$\frac{7}{5}$，
    ∴a=5x+10＞5×（-$\frac{7}{5}$）+10=3．
    ∴a的取值范围为a＞3．

    点评 本题考查了解一元一次不等式、一元一次方程的解以及一次函数的性质，解题的关键是得出a关于x的函数关系式．本题属于基础题，难度不大，解决该题型题目时，通过解方程得出a关于x的函数关系式是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．解不等式组：3≤2x-1≤7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．计算：$\sqrt{-3a}$÷$\sqrt{\frac{{a}^{2}}{2}}$=-$\frac{\sqrt{-6a}}{a}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

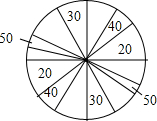    8．某商场搞促销活动，规定凡购物满200元就有一次摇奖机会，摇奖的转盘如图所示．转盘上写有礼券金额，其中20元、30元、40元、50元礼券所对应的扇形的圆心角之和依次为80°、60°、40°、20°．计算：
    （1）摇一次奖获得20元礼券的概率；
    （2）摇一次奖获得礼券大于30元的概率；
    （3）摇一次奖获得礼券的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如果关于x的不等式（2m-3）x＜3-2m的解集为x＞-1，则m＜$\frac{3}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

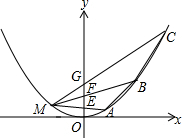    4．如图，M、A，B，C为抛物线y=ax2上不同的四点，M（-2，1），线段MA，MB，MC与y轴的交点分别为E，F，G．且EF=FG=1．
    （1）若F的坐标为（0，t），求点B的坐标（用t表示）；
    （2）若△AMB的面积是△BMC面积的$\frac{1}{2}$，求直线MB的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．对于实数x，y，若有$\sqrt{{x}^{2}-4}+|y+2|=0$，则x+y=0或-4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．先化简，再求值：$\frac{a-b}{a}$÷（a-$\frac{2ab-{b}^{2}}{a}$），其中a=2016，b=2015．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．解不等式组$\left\{\begin{array}{l}2x-1≤x+2，①\\ \frac{3x+1}{5}+2≥1．②\end{array}\right.$请结合题意填空，完成本题的解答．
    （Ⅰ）解不等式①，得x≤3；
    （Ⅱ）解不等式②，得x≥-2；
    （Ⅲ）把不等式①和②的解集在数轴上表示出来：
    （Ⅳ）原不等式组的解集为-2≤x≤3．

    查看答案和解析>>

    同步练习册答案