
��ͼ���ھ���ABCD�У�AB=6��AD= ����E��AD�����ȷֵ㣬��AE
����E��AD�����ȷֵ㣬��AE DE������E��EF��AB��BC��F����������DC��AB����P��Q�ֱ�������DC������AB�϶��㣬��P��ÿ��1����λ���ٶ�����ƽ�ƣ���ʼ�������PQA=60�㣬��P���˶���ʱ��Ϊ
DE������E��EF��AB��BC��F����������DC��AB����P��Q�ֱ�������DC������AB�϶��㣬��P��ÿ��1����λ���ٶ�����ƽ�ƣ���ʼ�������PQA=60�㣬��P���˶���ʱ��Ϊ ��
��
��1������Q���B�غ�ʱ����DP�ij��ȣ�
��2����AB���е�ΪN��PQ���߶�BE�ཻ�ڵ�M���Ƿ���ڵ�P��ʹ�� Ϊ���������Σ������ڣ���ֱ��д��ʱ��
Ϊ���������Σ������ڣ���ֱ��д��ʱ�� ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
��3����� ���ı���
���ı��� ���ص����ֵ����ΪS������S��
���ص����ֵ����ΪS������S�� �ĺ�����ϵʽ����Ӧ���Ա���
�ĺ�����ϵʽ����Ӧ���Ա��� ��ȡֵ��Χ��
��ȡֵ��Χ��
��1��3 ��2��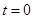 ��
�� 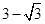 ��
�� 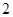 ��3��
��3��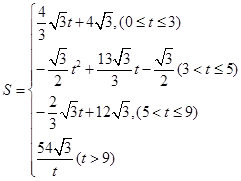
���������������������ͼ������������Уȴ�ֱ��AB��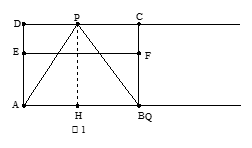
�ߡ�PQA=60�㣬AD=3 ��
��
��PH=3 ��
��
��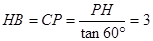 ��
��
��DP=DC��CP=6��3=3��
��2�����ڴ��ڵ�P��ʹ�� Ϊ����������
���������� ��
��  ��
��  ��
��
��3����� ���ı���
���ı��� ���ص����ֵ����ΪS
���ص����ֵ����ΪS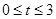 ��Q��B���غϣ�P����CD�ߵ��е㴦����ʱ��
��Q��B���غϣ�P����CD�ߵ��е㴦����ʱ�� �ǵȱ������Σ��������ı���
�ǵȱ������Σ��������ı��� ���ص����ֵ����S=
���ص����ֵ����S= ����
����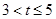 ʱ��
ʱ�� ���ı���
���ı��� ���ص����ֵ����S=
���ص����ֵ����S=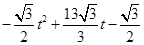 ����
����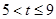 ����
���� ���ı���
���ı��� ���ص����ֵ����S=
���ص����ֵ����S=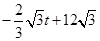 ����
����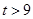 ����
���� ���ı���
���ı��� ���ص����ֵ����S=
���ص����ֵ����S=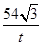 ������������
������������ ���ı���
���ı��� ���ص����ֵ����
���ص����ֵ����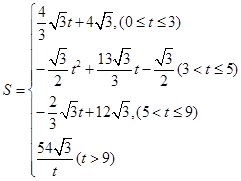
���㣺���Ǻ��������������Σ�������ϵʽ
���������⿼�����Ǻ��������������Σ�������ϵʽ��Ҫ��ѧ���������Ǻ����Ķ��壬���������ε����ʣ��������Ľ���ʽ�����⿼����֪ʶ�㣬�ѶȽϴ�


 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ���ھ���ABCD�У�AB=4cm��BC=8cm����P�ӵ�A������1cm/s���ٶ����B�˶�����Q�ӵ�B������2cm/s���ٶ����C�˶����辭����ʱ��Ϊxs����PBQ�����Ϊycm2��������ͼ���ܷ�ӳy��x֮��ĺ�����ϵ���ǣ�������
��ͼ���ھ���ABCD�У�AB=4cm��BC=8cm����P�ӵ�A������1cm/s���ٶ����B�˶�����Q�ӵ�B������2cm/s���ٶ����C�˶����辭����ʱ��Ϊxs����PBQ�����Ϊycm2��������ͼ���ܷ�ӳy��x֮��ĺ�����ϵ���ǣ�������A�� | B�� | C�� | D�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��
��| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 �������У�Q��ͣ����1s��ͼ����P��Q����������AB-BC-CD������·��S��cm����ʱ��t��s��֮��ĺ�����ϵͼ��
�������У�Q��ͣ����1s��ͼ����P��Q����������AB-BC-CD������·��S��cm����ʱ��t��s��֮��ĺ�����ϵͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AOB=60�㣬AB=6����AD=��������
��ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AOB=60�㣬AB=6����AD=���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 DE��EF��AB���ڵ�F����CE=x��BF=y��
DE��EF��AB���ڵ�F����CE=x��BF=y���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com