
| 3-m |
| 2 |
|
| 2 |
| 3 |
| 2 |
| 3 |


科目:初中数学 来源: 题型:
 甲、乙二人沿着相同的路线由A地到B地匀速行进.已知A、B两地间的路程为20km,他们行进的路程s(km)与行进的时间t(h)之间的函数关系如图所示.根据图象信息,下列说法不正确的是( )
甲、乙二人沿着相同的路线由A地到B地匀速行进.已知A、B两地间的路程为20km,他们行进的路程s(km)与行进的时间t(h)之间的函数关系如图所示.根据图象信息,下列说法不正确的是( )| A、甲的速度是5km/h |
| B、乙的速度是20km/h |
| C、乙比甲晚出发1h |
| D、甲走完全程比乙走完全程多用了2h |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、∠A>∠B>∠C |
| B、∠B>∠C>∠A |
| C、∠A>∠C>∠B |
| D、∠C>∠A>∠B |
查看答案和解析>>
科目:初中数学 来源: 题型:
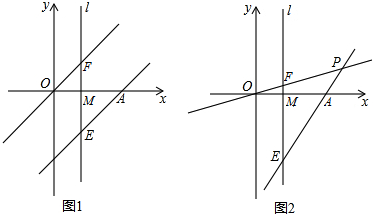
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,小明同学在南北方向的滨河路A处,测得体育馆P在北偏西30°方向上,向北前行500米到达B处,测得体育馆P在北偏西75°方向上,求体育馆P到滨河路的距离PC.(结果精确到0.1米,
如图,小明同学在南北方向的滨河路A处,测得体育馆P在北偏西30°方向上,向北前行500米到达B处,测得体育馆P在北偏西75°方向上,求体育馆P到滨河路的距离PC.(结果精确到0.1米,| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com