
 如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )
如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )| A. | △EBD是等腰三角形,EB=ED | B. | 折叠后∠ABE和∠C′BD一定相等 | ||
| C. | 折叠后得到的图形是轴对称图形 | D. | △EBA和△EDC′一定是全等三角形 |
分析 根据题意结合图形可以证明EB=ED,进而证明△ABE≌△C′DE;此时可以判断选项A、B、D是成立的,问题即可解决.
解答  解:由题意得:
解:由题意得:
△BC′D≌△BFD,
∴DC′=DF,∠C′=∠C=90°;
∠C′BD=∠CBD;
又∵四边形ABCD为矩形,
∴∠A=∠F=90°;DE∥BF,AB=DF;
∴∠EDB=∠FBD,DC′=AB;
∴∠EDB=∠C′BD,
∴EB=ED,△EBD为等腰三角形;
在△ABE与△CDE中,
∵$\left\{\begin{array}{l}{BE=DE}\\{AB=C′D}\end{array}\right.$,
∴△ABE≌△C′DE(HL);
又∵△EBD为等腰三角形,
∴折叠后得到的图形是轴对称图形;
综上所述,选项A、C、D成立,
∴下列说法错误的是B,
故选B.
点评 该命题主要考查了翻折变换及其应用问题;解题的关键是灵活运用翻折变换的性质,找出图中隐含的等量关系;借助矩形的性质、全等三角形的判定等几何知识来分析、判断、推理或解答


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
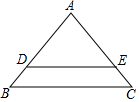 如图,点D,E分别是AB和AC上的点,△ADE∽△ABC,AD=2acm,DB=acm,BC=bcm,∠A=70°,∠B=50°.
如图,点D,E分别是AB和AC上的点,△ADE∽△ABC,AD=2acm,DB=acm,BC=bcm,∠A=70°,∠B=50°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 点A为线段BC外一动点,且BC=3,AB=1.如图所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
点A为线段BC外一动点,且BC=3,AB=1.如图所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 任何数都不等于它的相反数 | |
| B. | 符号相反的数互为相反数 | |
| C. | 若有理数a,b互为相反数,则它们一定异号 | |
| D. | 若有理数a,b互为相反数,那么a+b=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com