
若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=-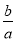 ,x1•x2=
,x1•x2=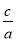 .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=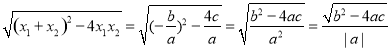 ;
;
参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
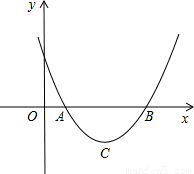
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
(1)4;(2)12.
【解析】
试题分析:(1)当△ABC为直角三角形时,由于AC=BC,所以△ABC为等腰直角三角形,过C作CE⊥AB于E,则AB=2CE.根据本题定理和结论,得到AB=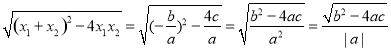 ,根据顶点坐标公式,得到CE=|
,根据顶点坐标公式,得到CE=|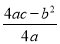 |=
|=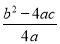 ,列出方程,解方程即可求出b2-4ac的值;
,列出方程,解方程即可求出b2-4ac的值;
(2)当△ABC为等边三角形时,解直角△ACE,得CE=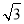 AE=
AE=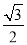 AB,据此列出方程,解方程即可求出b2-4ac的值.
AB,据此列出方程,解方程即可求出b2-4ac的值.
试题解析:(1)当△ABC为直角三角形时,过C作CE⊥AB于E,则AB=2CE.
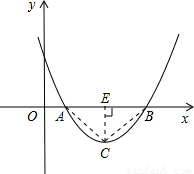
∵抛物线与x轴有两个交点,
∴△=b2-4ac>0,则|b2-4ac|=b2-4ac.
∵a>0,
∴AB=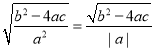 ,
,
又∵CE=|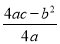 |=
|=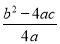 ,
,
∴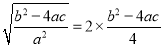 ,
,
∴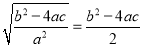 ,
,
∴b2-4ac= ,
,
∵b2-4ac>0,
∴b2-4ac=4;
(2)当△ABC为等边三角形时,
由(1)可知CE=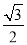 AB,
AB,
∴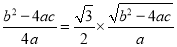 ,
,
∵b2-4ac>0,
∴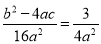 ,
,
∴b2-4ac=12.
考点:1.抛物线与x轴的交点;2.根与系数的关系;3.等腰三角形的性质;4.等边三角形的性质.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源:2014-2015学年安徽省心学校九年级上学期数学试卷(解析版) 题型:解答题
已知二次函数y=-2x2+4x+6
(1)求函数图象的顶点坐标及对称轴
(2)求此抛物线与x轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省七年级上学期期中检测数学试卷(解析版) 题型:选择题
下列各数中:+5、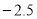 、
、 、2、
、2、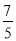 、
、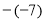 、0、-
、0、- 负有理数有 ( )
负有理数有 ( )
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川中江县继光实验学校九年级上期末模拟考试数学试卷(解析版) 题型:选择题
如图,在边长为3的正方形ABCD中,⊙O1与⊙O2外切,且⊙O1分别与DA、DC边相切,⊙O2分别与BA、BC边相切,则圆心距O1 O2为 .
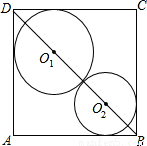
A.6-3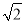 B.2.4 C.4-2
B.2.4 C.4-2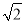 D.
D.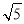 -1
-1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川中江县继光实验学校九年级上期末模拟考试数学试卷(解析版) 题型:选择题
如果两圆的半径分别是4和7,两圆的连心线段长为3,则两圆的位置关系( )
A、外离 B、内含 C、外切 D、内切
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省自贡市九年级上学期期末统一考试数学试卷(解析版) 题型:选择题
如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )

查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省凉山州九年级上学期期末数学试卷(解析版) 题型:填空题
在平面直角坐标系xOy中,以原点O为圆心半径为10的圆,直线y=mx-4m+3与⊙O交于A、B两点,则弦AB的长的最小值为
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省泰安市九年级第二次月考数学试卷(解析版) 题型:选择题
对于任意实数k,关于x的方程程x2-2(k+1)x-k2+2k-1=0的根的情况为
A.有两个相等的实数根 B.没有实数根
C.有两个不相等的实数根 D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com