
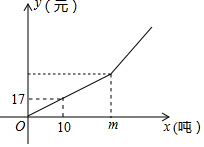
 为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:| 月份 | 用水量x(吨) | 水费y(元) |
| 四月 | 35 | 59.5 |
| 五月 | 80 | 151 |
分析 (1)根据单价=总价÷数量求出不超过m吨时水费的单价,结合五月的用水量及水费钱数,即可得出关于m的一元二次方程,解之即可得出m的值,再根据四月的用水量及水费钱数,即可确定m值;
(2)根据总价=单价×数量,即可求出y与x之间的函数关系式.
解答 解:(1)不超过m吨时,每吨水费为17÷10=1.7(元),
根据题意得:80×1.7+(80-m)×$\frac{m}{100}$=151,
整理得:m2-80m+1500=0,
解得:m1=30,m2=50.
∵35×1.7=59.5,
∴m≥35,
∴m=50.
(2)根据题意得:当0≤x≤50时,y=1.7x;
当x>50时,y=50×1.7+(x-50)×(1.7+$\frac{50}{100}$)=2.2x-25.
∴y与x之间的函数关系式为y=$\left\{\begin{array}{l}{1.7x(0≤x≤50)}\\{2.2x-25(x>50)}\end{array}\right.$.
点评 本题考查了一次函数的应用以及一元二次方程的应用,解题的关键是:(1)由五月的用水量及水费钱数,列出关于m的一元二次方程;(2)根据总价=单价×数量,求出y与x之间的函数关系式.


科目:初中数学 来源: 题型:解答题
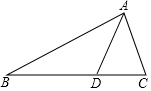 如图,在△ABC中,AC=4,D为BC边上的一点,CD=2,且△ADC与△ABD的面积比为1:3.
如图,在△ABC中,AC=4,D为BC边上的一点,CD=2,且△ADC与△ABD的面积比为1:3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
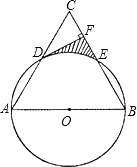 已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.
已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
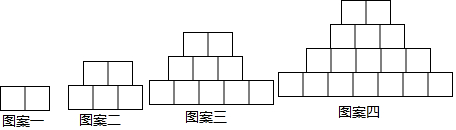
| A. | 902 | B. | 901 | C. | 900 | D. | 899 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com