
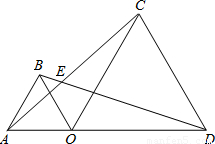
 已知点O为线段AD上一点,分别以AO、DO为边在线段的同侧作等边△OAB和等边△ODC,连接AC、BD相交于点E,求∠AEB的大小.
已知点O为线段AD上一点,分别以AO、DO为边在线段的同侧作等边△OAB和等边△ODC,连接AC、BD相交于点E,求∠AEB的大小.
|


科目:初中数学 来源:2008-2009学年广东省揭阳市揭东县竞智中学九年级(上)期中数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中AB=AC,BC=6,点D是BC的中点,连接AD,AD=4,
AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)试判断四![]() 边形ADCE的形状并说明理由.
边形ADCE的形状并说明理由.
(2)已知点P为线段AD上的动点,求PE+PC的最小值。
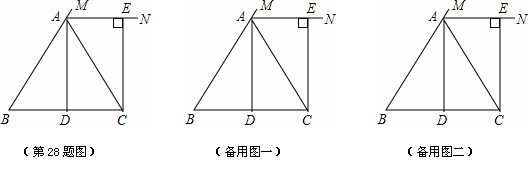 (3)已知有两个动点G,Q,其中G点在线段CE上运动,Q点在线段BD上运动,线段GQ的中点为R,求动点R所在区域的面积。
(3)已知有两个动点G,Q,其中G点在线段CE上运动,Q点在线段BD上运动,线段GQ的中点为R,求动点R所在区域的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com