
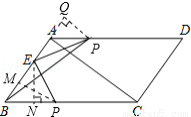
如图,□ABCD中,AC⊥AB ,AB=3cm,BC=5cm,点E为AB上一点,且AE=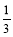 AB.点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止. 则当运动时间为 秒时,△BEP为等腰三角形.
AB.点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止. 则当运动时间为 秒时,△BEP为等腰三角形.

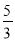 ,2,
,2, ,
,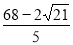
【解析】
试题分析:∵∠BAC=90°,BC=5cm,AB=3cm,′
由勾股定理得:AC=4cm,
即AB、CD间的最短距离是4cm,
∵AB=3cm,AE= AB,
AB,
∴AE=1cm,BE=2cm,
设经过ts时,△BEP是等腰三角形,
当P在BC上时,
①BP=EB=2cm,
t=2时,△BEP是等腰三角形;
②BP=PE,
作PM⊥AB于M,
∴BM=ME= BE=1cm
BE=1cm
∵cos∠ABC=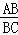 =
=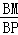 =
=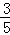 ,
,
∴BP=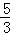 cm,
cm,
t=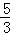 时,△BEP是等腰三角形;
时,△BEP是等腰三角形;
③BE=PE=2cm,
作EN⊥BC于N,则BP=2BN,
∴cosB=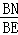 =
=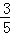 ,
,
∴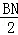 =
=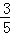 ,
,
BN=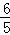 cm,
cm,
∴BP=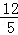 ,
,
∴t=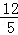 时,△BEP是等腰三角形;
时,△BEP是等腰三角形;
当P在CD上不能得出等腰三角形,
∵AB、CD间的最短距离是4cm,CA⊥AB,CA=4cm,
当P在AD上时,只能BE=EP=2cm,
过P作PQ⊥BA于Q,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠QAD=∠ABC,
∵∠BAC=∠Q=90°,
∴△QAP∽△ABC,
∴PQ:AQ:AP=4:3:5,
设PQ=4xcm,AQ=3xcm,
在△EPQ中,由勾股定理得:(3x+1)2+(4x)2=22,
∴x=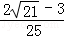 ,
,
AP=5x= cm,
cm,
∴t=5+5+3﹣ =
=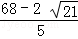 ,
,
答:从运动开始经过2s或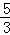 s或
s或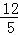 s或
s或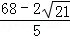 s时,△BEP为等腰三角形.
s时,△BEP为等腰三角形.
考点: 平行四边形综合题


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,平面直角坐标系中,以点C(2, )为圆心,以2为半径的圆与x轴交于A,B两点.
)为圆心,以2为半径的圆与x轴交于A,B两点.

(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:选择题
已知反比例函数 的图象经过点(
的图象经过点( ),则此反比例函数的图象在( )
),则此反比例函数的图象在( )
A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省丽水市莲都区九年级第一次中考模拟数学试卷(解析版) 题型:解答题
(本题8分)一列快车由甲地开往乙地,一列慢车由乙地开往甲地, 两车同时出发,沿同一条道路匀速行驶.设行驶时间为t(h),两车之间的距离为s(km),图中折线A-B-C-D表示s与t之间的函数关系.
(1)甲、乙两地相距 km,两车出发后 h相遇;
(2)通过计算说明,当快车到达乙地时,慢车还要多少时间才能到达甲地?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级直升班第一次综合测试数学试卷(解析版) 题型:填空题
如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com