
如图,PB切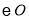 于点B,联结PO并延长交
于点B,联结PO并延长交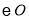 于点E,过点B作BA⊥PE交
于点E,过点B作BA⊥PE交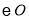 于点A,联结AP,AE.
于点A,联结AP,AE.

(1)求证:PA是 的切线;
的切线;
(2)如果OD=3,tan∠AEP=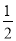 ,求
,求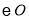 的半径.
的半径.
(1)证明见试题解析;(2)5.
【解析】
试题分析:(1)连接OA、OB,根据垂径定理得出AB⊥OP,推出AP=BP,∠APO=∠BPO,证△PAO≌△PBO,推出∠PBO=∠PAO=90°,根据切线的判定推出即可;
(2)在Rt△ADE中,由tan∠AEP=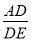 =
=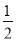 ,设AD=x,DE=2x,则OE=2x—3,在Rt△AOD中,由勾股定理,得
,设AD=x,DE=2x,则OE=2x—3,在Rt△AOD中,由勾股定理,得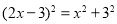 .解出x,则可以求出⊙O的半径的长.
.解出x,则可以求出⊙O的半径的长.
试题解析:(1)证明:如图,联结OA,OB .∵PB是⊙O的切线,∴ ∠PBO=90°.∵ OA=OB,BA⊥PE于点D,∴ ∠POA=∠POB.又∵ PO=PO,∴ △PAO≌△PBO.∴ ∠PAO=∠PBO=90°.∴PA⊥OA.∴ 直线PA为⊙O的切线;

(2)在Rt△ADE中,∠ADE=90°,∵tan∠AEP=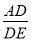 =
=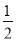 ,∴设AD=x,DE=2x,∴OE=2x—3,在Rt△AOD中,由勾股定理,得
,∴设AD=x,DE=2x,∴OE=2x—3,在Rt△AOD中,由勾股定理,得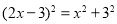 .解得,
.解得,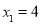 ,
,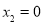 (不合题意,舍去).∴ AD=4,OA=OE=2x-3=5.即⊙O的半径的长5.
(不合题意,舍去).∴ AD=4,OA=OE=2x-3=5.即⊙O的半径的长5.
考点:切线的判定与性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年北京市顺义区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知抛物线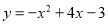 .(1)求出这个抛物线的对称轴和顶点坐标;(2)在给定的坐标系中画出这个抛物线,若抛物线与x轴交于A,B两点,与y轴交于点C,求△ABC的面积.
.(1)求出这个抛物线的对称轴和顶点坐标;(2)在给定的坐标系中画出这个抛物线,若抛物线与x轴交于A,B两点,与y轴交于点C,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市海淀区九年级上学期期末考试数学试卷(解析版) 题型:解答题
在平面直角坐标系xOy中,设点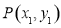 ,
,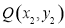 是图形W上的任意两点.
是图形W上的任意两点.
定义图形W的测度面积:若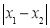 的最大值为m,
的最大值为m,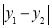 的最大值为n,则
的最大值为n,则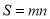 为图形W的测度面积.
为图形W的测度面积.
例如,若图形W是半径为1的⊙O.当P,Q分别是⊙O与x轴的交点时,如图1,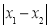 取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,
取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,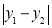 取得最大值,且最大值n=2.则图形W的测度面积
取得最大值,且最大值n=2.则图形W的测度面积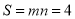 .
.
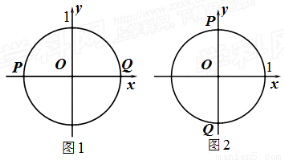
(1)若图形W是等腰直角三角形ABO,OA=OB=1.
①如图3,当点A,B在坐标轴上时,它的测度面积S= ;
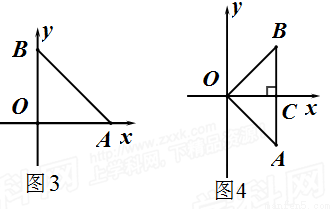
②如图4,当AB⊥x轴时,它的测度面积S= ;
(2)若图形W是一个边长为1的正方形ABCD,则此图形测度面积S的最大值为 ;
(3)若图形W是一个边长分别为3和4的矩形ABCD,求它的测度面积S的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市海淀区九年级上学期期末考试数学试卷(解析版) 题型:选择题
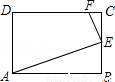
如图,已知矩形ABCD的长AB为5,宽BC为4,E是BC边上的一个动点,AE⊥EF,EF交CD于点F.设BE=x,FC=y,则点E从点B运动到点C时,能表示y关于x的函数关系的大致图象是( )
A.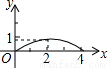 B.
B.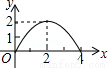 C.
C.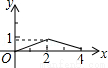 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市海淀区九年级上学期期末考试数学试卷(解析版) 题型:选择题
方程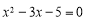 的根的情况是( )
的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定是否有实数根
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市丰台区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知二次函数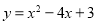 .
.

(1)把这个二次函数化成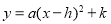 的形式;
的形式;
(2)画出这个二次函数的图象,并利用图象写出当x为何值时,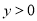 .
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市丰台区九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,在△ABC中,点D,E分别在AB,AC边上,且 DE∥BC,如果AD∶DB=3∶2, EC=4,那么AE的长等于 .
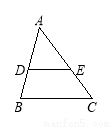
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.求线段EC的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com