
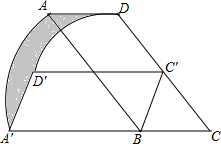
 如图,在?ABCD中,∠BCD=60°,AB=2BC=4,将?ABCD绕点B逆时针旋转一定角度后得到?A′BC′D′,其中点C的对应点C′落在边CD上,则图中阴影部分的面积.
如图,在?ABCD中,∠BCD=60°,AB=2BC=4,将?ABCD绕点B逆时针旋转一定角度后得到?A′BC′D′,其中点C的对应点C′落在边CD上,则图中阴影部分的面积. 分析 由旋转可得CB=C′B,根据∠C=60°可得△BCC′为等边三角形、△BCD为直角三角形,继而可得旋转角∠ABA′=∠DBD′=∠CBC′=60°,BD=2$\sqrt{3}$,最后根据阴影部分的面积=S扇形BAA′-S扇形BDD′计算可得.
解答 解:如图,连接BD、BD′,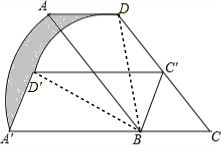
∵?A′BC′D′是由?ABCD绕点B旋转得到的,
∴∠ABA′=∠CBC′=∠DBD′,AB=A′B,CB=C′B,BD=BD′,
∵∠BCD=60°,AB=2BC=4,
∴BC′=BC=2=$\frac{1}{2}$AB=$\frac{1}{2}$CD,
∴△BCD是直角三角形,∠ABA′=∠CBC′=∠DBD′=60°,
∴BD=$\sqrt{C{D}^{2}-B{C}^{2}}$=2$\sqrt{3}$,
则阴影部分的面积=S扇形BAA′-S扇形BDD′
=$\frac{60•π•{4}^{2}}{360}$-$\frac{60•π•(2\sqrt{3})^{2}}{360}$
=$\frac{2}{3}$π.
点评 本题主要考查旋转的性质、平行四边形的性质、勾股定理、等边三角形等知识点,根据已知条件求得旋转半径和旋转角是求扇形面积的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | C. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{12}$÷2=$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$和-4互为相反数 | B. | $\frac{1}{4}$和-4互为倒数 | ||
| C. | 0.1和10互为倒数 | D. | 0的倒数是0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
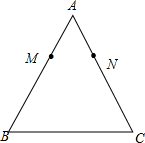 (1)下列仅用无刻度的直尺就能完成作图的是②(填写序号即可)
(1)下列仅用无刻度的直尺就能完成作图的是②(填写序号即可)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6个单位长度 | B. | 4个单位长度 | C. | 2个单位长度 | D. | 2$\sqrt{5}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com