
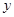 (个)与销售时间
(个)与销售时间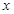 (天)之间有如下关系:
(天)之间有如下关系: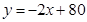 (
(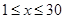 ,且
,且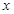 为整数);又知销售价格
为整数);又知销售价格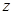 (元/个)与销售时间
(元/个)与销售时间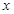 (天)之间的函数关系满足如图所示的函数图像.
(天)之间的函数关系满足如图所示的函数图像.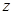 关于
关于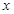 的函数关系式;
的函数关系式;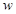 (元)与销售时间
(元)与销售时间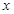 (天)之间的函数关系式;
(天)之间的函数关系式; 而日销售量就比9月30日提高了
而日销售量就比9月30日提高了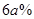 (其中
(其中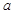 为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求
为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求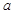 的值.
的值. (参考数据:
(参考数据: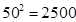 ,
,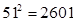 ,
, )
)











科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
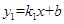 和反比例函数
和反比例函数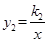 (
(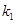 ?
?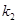 ≠0)的图像如图所示,若
≠0)的图像如图所示,若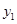 >
>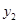 ,则
,则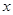 的取值范围是( ).
的取值范围是( ).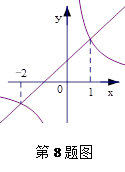
A.-2<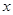 <0或 <0或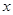 >1 >1 | B.-2<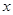 <1 <1 | C.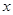 <-2或 <-2或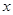 >1 >1 | D.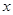 <-2或0< <-2或0<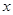 <1 <1 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
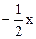 +1与x轴、y轴的交点
+1与x轴、y轴的交点
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
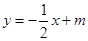 与x轴、y轴分别交于A、B两点,且点B的坐标为(0,8).(1)求m的值;(2)设直线OP与线段AB相交于P点,且
与x轴、y轴分别交于A、B两点,且点B的坐标为(0,8).(1)求m的值;(2)设直线OP与线段AB相交于P点,且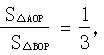 ,试求点P的坐标.
,试求点P的坐标.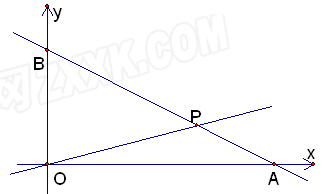
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com