
【题目】如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=34°,∠AEB=72°.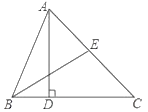
(1)求∠CAD和∠BAD的度数;
(2)若点F为线段BC上任意一点,当△EFC为直角三角形时,试求∠BEF的度数.
【答案】
(1)解:∵BE为△ABC的角平分线,
∴∠CBE=∠EBA=34°,
∵∠AEB=∠CBE+∠C,
∴∠C=72°﹣34°=38°,
∵AD为△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=52°,
∠BAD=90°-∠ABD=90°-68°=22°
(2)解:当∠EFC=90°时,∠BEF=90°﹣∠CBE=56°,
当∠FEC=90°时,∠BEF=180°-72°﹣90°=18°
【解析】(1)由BE为∠ABC的平分线,得出∠BAD=22°,再求出∠C,得出∠CAD=52°,即可得出结论;
(2)分两种情况:①当∠EFC=90°时;②当∠FEC=90°时;由角的互余关系和三角形的外角性质即可求出∠BEF的度数.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握垂线的性质(垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短)的相关知识才是答题的关键.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中,下列说法正确的是( )
A.数100和η,t都是变量
B.数100和η都是常量
C.η和t是变量
D.数100和t都是常量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图线段AB=9,C、D、E分别为线段AB(端点A、B除外)上顺次三个不同的点,图中所有的线段和等于46,则下列结论一定成立的是( ) ![]()
A.CD=3
B.DE=2
C.CE=5
D.EB=5
查看答案和解析>>
科目:初中数学 来源: 题型:
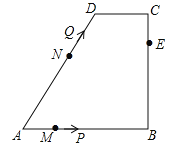
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB﹣BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND﹣DC﹣CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t秒,则S与t函数关系的大致图象为( )
A. B.
B.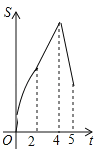 C.
C.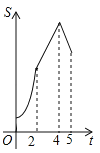 D.
D.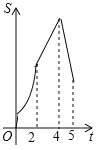
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com