
 在Rt△ABC中,∠ABC=45°,F为BC中点,BE平分∠ABC交AF于G,交AC于E,CD⊥BE于D.有以下判断:①BF=CF;②∠ABE=∠DCE;③AE=AG;④BE=2CD;⑤CE=$\sqrt{2}$AG;⑥CE=BG.其中正确的判断个数是( )
在Rt△ABC中,∠ABC=45°,F为BC中点,BE平分∠ABC交AF于G,交AC于E,CD⊥BE于D.有以下判断:①BF=CF;②∠ABE=∠DCE;③AE=AG;④BE=2CD;⑤CE=$\sqrt{2}$AG;⑥CE=BG.其中正确的判断个数是( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
分析 由中点的定义得出①正确;由直角三角形的性质和对顶角相等得出②正确;由角平分线的定义和三角形内角和定理得出∠AGE=∠AEG,证出AE=AG,③正确;连接AD,证明点A、B、C、D四点共圆,由圆周角定理得出∠ABD=∠ACD,∠DAC=∠DBC,证出∠DAC=∠ACD,得出AD=CD,取BE的中点H,连接AH,由直角三角形斜边上的中线性质得出AH=BH=$\frac{1}{2}$BE,得出∠HAB=∠HBA,证出∠ADB=∠AHD,得出AD=AH=CD,证出④正确;证明△ABE∽△DBC,得出$\frac{AG}{BE}$=$\frac{CD}{\sqrt{2}AB}$,再证明△ABE∽△DCE,得出$\frac{CD}{AB}$=$\frac{CE}{BE}$,即可得出CE=$\sqrt{2}$AG,⑤正确;证明△BFG∽△CDE,得出$\frac{BG}{CE}=\frac{BF}{CD}$,由BF=$\frac{1}{2}$BC>$\frac{1}{2}$BE=CD,得出BG>CE,⑥不正确;即可得出结论.
解答 解:∵F为BC中点,
∴BF=CF,故①正确;
∵∠BAC=90°,CD⊥BE,
∴∠BAE=∠CDE=90°,
∵∠AEB=∠DEC,
∴∠ABE=∠DCE,故②正确;
∵∠ABC=45°,BE平分∠ABC,
∴∠ABE=22.5°,
∴∠AEG=90°-22.5°=67.5°,
∵Rt△ABC中,∠ABC=45°,
∴AB=AC,
∵F为BC中点,
∴∠FAE=∠FAB=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×90°=45°,
∴∠AGE=180°-∠GAE-∠AEG=180°-45°-67.5°=67.5°,
∴∠AGE=∠AEG,
∴AE=AG,故③正确;
连接AD,如图所示:
∵∠BAC=∠BDC=90°,
∴点A、B、C、D四点共圆,
∴∠ABD=∠ACD,∠DAC=∠DBC,
∵∠ABD=∠DBC,
∴∠DAC=∠ACD,
∴AD=CD,取BE的中点H,连接AH,
∴AH=BH=$\frac{1}{2}$BE,
∴∠HAB=∠HBA,
∴∠AHE=∠HAB+∠ABH=2∠ABE=45°,
∵∠ADB=∠ACB=45°,
∴∠ADB=∠AHD,
∴AD=AH=CD,
∴BE=2CD,故④正确;
∵∠BAE=∠CDB=90°,∠ABE=∠DBC,
∴△ABE∽△DBC,
∴$\frac{AE}{CD}$=$\frac{BE}{BC}$,
∵AE=AG,BC=$\sqrt{2}$AB,
∴$\frac{AG}{BE}$=$\frac{CD}{\sqrt{2}AB}$,
∵∠BAE=∠CDB=90°,∠ABE=∠DCE,
∴△ABE∽△DCE,
∴$\frac{CD}{AB}$=$\frac{CE}{BE}$,
∴$\frac{AG}{BE}$=$\frac{CE}{\sqrt{2}BE}$,
∴CE=$\sqrt{2}$AG,
故⑤正确;
∵在Rt△ABC中,∠ABC=45°,
∴△ABC是等腰直角三角形,
∵F是BC的中点,
∴AF⊥BC,
∴∠BFG=90°=∠D,
∵∠ABD=∠ACD,∠ABD=∠DBC,
∴DBC=∠ACD,
∴△BFG∽△CDE,
∴$\frac{BG}{CE}=\frac{BF}{CD}$,
∵BF=$\frac{1}{2}$BC>$\frac{1}{2}$BE=CD,
∴BG>CE,
∴⑥不正确;
正确的个数有5个,
故选:C.
点评 本题考查了等腰直角三角形的判定与性质、相似三角形的判定与性质、四点共圆、圆周角定理、直角三角形斜边上的中线等知识;本题综合性强,难度较大,熟记等腰三角形的性质和证明三角形相似是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批灯泡的使用寿命看是否合格 | |
| B. | 了解渠江河中鱼的种类 | |
| C. | 了解中央电视台《新闻联播》的收视率 | |
| D. | 了解七年级一班学生的视力状况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下面的材料:
阅读下面的材料:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,-3) | B. | (2,-2) | C. | (3,-3) | D. | (2,-4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片七年级下学期第一次月考数学试卷(解析版) 题型:单选题
下面是一名学生所做的4道练习题:
①(-3)0=1;② a3+a3=a6; ③ 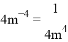 ;④ (xy 2) 3 = x 3y 6,他做对的个数是 ( )
;④ (xy 2) 3 = x 3y 6,他做对的个数是 ( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com