
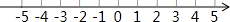 (1)计算:|-$\sqrt{2}$|+(π-3)0+($\frac{1}{2}$)-1-2cos45°
(1)计算:|-$\sqrt{2}$|+(π-3)0+($\frac{1}{2}$)-1-2cos45°分析 (1)先去掉绝对值,用零指数幂,负指数幂,三角函数,化简,最后用实数的运算即可.
(2)分别解出不等式①,②的解集确定出公共部分即可.
解答 解:(1)|-$\sqrt{2}$|+(π-3)0+($\frac{1}{2}$)-1-2cos45°
=$\sqrt{2}$+1+2-2×$\frac{\sqrt{2}}{2}$
=$\sqrt{2}$+1+2-$\sqrt{2}$
=3,
(2)$\left\{\begin{array}{l}{2x-1>x+1①}\\{x+8>4x-1②}\end{array}\right.$
解不等式①,得,x>2,
解不等式②,得,x<3
∴原不等式组的解集为2<x<3.
∴原不等式组的解集在数轴上表示如图所示: .
.
点评 此题是实数的运算,主要考查了实数的运算,零指数幂的运算,负整数指数幂的运算,特殊三角函数值,要熟练掌握,解本题的关键是熟练掌握实数的运算顺序.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线l1:y=-x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,-2).
已知抛物线l1:y=-x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 数形结合 | B. | 换元与降次 | C. | 消元 | D. | 公理化 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
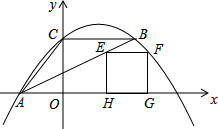 如图,△ABC中,点A在x轴上,点C在y轴上,BC∥x轴,AB平分∠CAO,二次函数y=ax2-5ax+4的图象经过△ABC的三个顶点.
如图,△ABC中,点A在x轴上,点C在y轴上,BC∥x轴,AB平分∠CAO,二次函数y=ax2-5ax+4的图象经过△ABC的三个顶点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
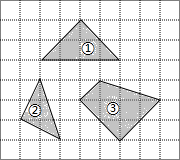 如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③)的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是( )
如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③)的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是( )| A. | 只有② | B. | 只有③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com