Question

15．如下图所示，AB是半圆的直径，O是AB的中点．正方形CDEF的面积为4平方厘米（F、E在圆上，C、D在AB上），四边形DPNM也是正方形（M为DE上一点，N为$\widehat{BE}$上一点），连接NE、MF，则图中阴影部分的面积是$\frac{13}{2}$-$\sqrt{15}$平方厘米．

Answer 1

分析 连接OE，ON，过OH⊥EF于H，根据垂径定理得到OD=HE，根据已知条件得到DE=2，EH=1，根据勾股定理得到OE=$\sqrt{5}$，根据勾股定理得到x=$\frac{\sqrt{15}-1}{2}$，求得EM=2-$\frac{\sqrt{15}-1}{2}$，于是得到结论．

解答 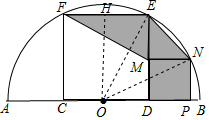解：连接OE，ON，过OH⊥EF于H，
∴EH=FH，
∴OD=HE，
∵正方形CDEF的面积为4平方厘米
∴DE=2，EH=1，
∴OE=$\sqrt{5}$，
∴ON=$\sqrt{5}$，
设PD=x，
∴（1+x）²+x²=5，
∴x=$\frac{\sqrt{15}-1}{2}$，
∴EM=2-$\frac{\sqrt{15}-1}{2}$，
∴图中阴影部分的面积=S_{正方形DMNP}+S_△MEN+S_△EFM
=（$\frac{\sqrt{15}-1}{2}$）²+$\frac{1}{2}×$（$\frac{\sqrt{15}-1}{2}$）×（2-$\frac{\sqrt{15}-1}{2}$）+$\frac{1}{2}×$2×（2-$\frac{\sqrt{15}-1}{2}$）=$\frac{13}{2}$-$\sqrt{15}$，
故答案为：$\frac{13}{2}$-$\sqrt{15}$．

点评 本题考查了正方形的性质，垂径定理，勾股定理，三角形面积的计算，正确的作出辅助线是解题的关键．