解:(1)∵AB∥CD,DP是∠CDG的平分线,
∴∠CDA=∠A=40°,∠CDP=∠PDA=20°;
同理,∠PAB=∠CBP=39°
在△CDM中,∠DMG=∠CDM+∠C=78°+20°=98°,
在△BPM中,根据三角形的外角的性质可以得到:∠P=∠DMG-∠PBM=98°-39°=59°;
(2)∵AB∥CD
∴∠ABP=∠PBC=

∠C
在△CDM和△PBM中,根据三角形的外角的性质,即可得到:∠DMB=∠C+

α=∠P+∠PBC
即:∠C+

α=β+

∠C
则∠C=2β-α.
分析:(1)根据三角形的外角的性质,外角等于不相邻的两个内角的和以及平行线、角平分线的性质即可求解;
(2)根据外角等于不相邻的两个内角的和可以求解.
点评:本题主要考查了三角形的外角等于不相邻的两个内角的和,平行线和角平分线的性质,结合图形找出各角间的关系是解题的关键.

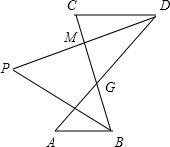 已知AB∥CD
已知AB∥CD ∠C
∠C α=∠P+∠PBC
α=∠P+∠PBC α=β+
α=β+ ∠C
∠C
