Question

1．如图，⊙O的半径为6，弦AB=10，M是弦AB上的动点，量线段OM的最小值为最大值为$\sqrt{11}$和6．

Answer 1

分析 过O作OM′⊥AB，连接OA，由“过直线外一点与直线上的所有连线中垂线段最短”的知识可知，当OM于OM′重合时OM最短，由垂径定理可得出AM′的长，再根据勾股定理可求出OM′的长，即线段OM长的最小值．

解答 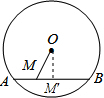解：如图所示，
过O作OM′⊥AB，连接OA，
∵过直线外一点与直线上的所有连线中垂线段最短，
∴当OM于OM′重合时OM最短，
∵AB=10，OA=6，
∴AM′=$\frac{1}{2}$×10=5，
∴在Rt△OAM′中，OM′=$\sqrt{O{A}^{2}-AM{′}^{2}}$=$\sqrt{11}$，
∴线段OM长的最小值为$\sqrt{11}$，最大值为6．
故答案为：$\sqrt{11}$和6．

点评 本题考查的是垂径定理，熟知平分弦的直径平分这条弦，并且平分弦所对的两条弧是解答此题的关键．