
| A. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ | B. | ∠B=∠A+∠C | C. | (b+a)(b-a)=c2 | D. | ∠A:∠B:∠C=5:3:2 |
分析 由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方或最大角是否是90°即可.
解答 解:A、∵($\frac{1}{5}$)2+($\frac{1}{4}$)2≠($\frac{1}{3}$)2,故不能判定是直角三角形;
B、∵∠B=∠A+∠C,∴∠B=90°,故是直角三角形,正确;
C、∵(b+a)(b-a)=c2,∴b2-a2=c2,即a2+c2=b2,故是直角三角形,正确;
D、∵∠A:∠B:∠C=5:3:2,∴∠A=180°×$\frac{5}{10}$=90°,故是直角三角形,正确.
故选A.
点评 本题主要考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.


科目:初中数学 来源: 题型:解答题
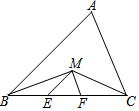 如图,M是∠ABC与∠ACB的平分线的交点,ME∥AB交BC于E,MF∥AC交BC于F,那么△MEF周长与已知△ABC的边BC有何关系?请你说明理由.
如图,M是∠ABC与∠ACB的平分线的交点,ME∥AB交BC于E,MF∥AC交BC于F,那么△MEF周长与已知△ABC的边BC有何关系?请你说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4(1-x)2=4.84 | B. | 4(1+x)2=4.84 | C. | (1+x)2=4.84-4 | D. | 4×2x=4.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 100y+x | B. | 100x+y | C. | x+y | D. | yx |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3\frac{1}{16}}$=$\frac{7}{4}$ | B. | $\sqrt{\frac{2y}{3x}}$=$\frac{1}{3x}$$\sqrt{6xy}$ | C. | $\sqrt{(\frac{1}{4})^{2}-(\frac{1}{5})^{2}}$=$\frac{1}{20}$ | D. | $\sqrt{\frac{4}{9x}}$=$\frac{2\sqrt{x}}{3x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com