Question

⊙O的半径为10cm，两平行弦AC，BD的长分别为12cm，16cm，则两弦间的距离是

1. A.
   2cm
2. B.
   14cm
3. C.
   6cm或8cm
4. D.
   2cm或14cm

Answer 1

D
分析：解答有关垂径定理的题，作辅助线一般是连接半径或作垂直于弦的直径．分两种情况解答：①弦AC、BD在⊙O的同侧；②弦AC、BD在⊙O的两侧．
解答：如图①

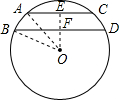
作OE⊥AC垂足为E，交BD于点F，
∵OE⊥AC AC∥BD，
∴OF⊥BD，
∴AE=AC=6cm BF=BD=8cm，
在Rt△AOE中
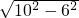
OE===8cm
同理可得：
OF=6cm
∴EF=OE-OF=8-6=2cm；
如图②

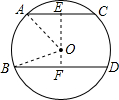
同理可得：EF=OE+OF=8+6=14cm
综上所述两弦之间的距离为2cm或14cm．
故选D．
点评：此题主要利用垂径定理，把问题转化为直角三角形，运用勾股定理来解决，还得注意分情况讨论．