
【题目】早晨,小明步行到离家900米的学校去上学,到学校时发现眼镜忘在家中,于是他立即按原路步行回家,拿到眼镜后立即按原路骑自行车返回学校.已知小明步行从学校到家所用的时间比他骑自行车从家到学校所用的时间多10分钟,小明骑自行车速度是步行速度的3倍.
(1)求小明步行速度(单位:米/分)是多少;
(2)下午放学后,小明骑自行车回到家,然后步行去图书馆,如果小明骑自行车和步行的速度不变,小明步行从家到图书馆的时间不超过骑自行车从学校到家时间的2倍,那么小明家与图书馆之间的路程最多是多少米?
科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC的周长是10,求□ABCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产A、B两种产品共50件,其生产成本与利润如下表:
A种产品 | B种产品 | |
成本 (万元/件) | 0.6 | 0.9 |
利润 (万元/件) | 0.2 | 0.4 |
若该工厂计划投入资金不超过40万元,且希望获利超过16万元,问工厂有哪几种生产方案?哪种生产方案获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.
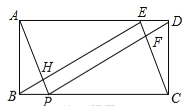
(1)断⊿BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对九(1)班学生进行百米测验,已知女生达标成绩为18秒,下面两图分别是甲、乙两小组各5名女生的成绩统计图.请你根据下面统计图回答问题.
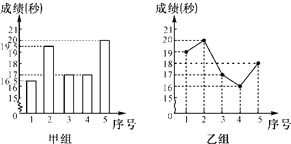
(1)甲、乙两组的达标率分别是多少?
(2)根据图中信息你认为哪个组的成绩相对稳定?
(3)如果老师表扬甲组的成绩好于乙组,那么老师是从各组的平均数、中位数、达标率、方差中的哪个数来说明的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如表:
成绩(分) | 35 | 39 | 42 | 44 | 45 | 48 | 50 |
人数(人) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根据表中的信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是45分
C.该班学生这次考试成绩的中位数是45分
D.该班学生这次考试成绩的平均数是45分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点![]() ,
,![]() 满足
满足![]() .
.
![]() 则C点的坐标为______;A点的坐标为______.
则C点的坐标为______;A点的坐标为______.
![]() 已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束
已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束![]() 的中点D的坐标是
的中点D的坐标是![]() ,设运动时间为
,设运动时间为![]() 秒
秒![]() 问:是否存在这样的t,使
问:是否存在这样的t,使![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
![]() 点F是线段AC上一点,满足
点F是线段AC上一点,满足![]() ,点G是第二象限中一点,连OG,使得
,点G是第二象限中一点,连OG,使得![]() 点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,
点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,![]() 的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S= ![]() (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p= ![]() ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5
∴p= ![]() =6
=6
∴S= ![]() =
= ![]() =6
=6
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com