
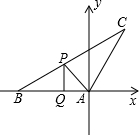
 (2013•唐山一模)如图,△ABC中,P是BC上一点,PQ⊥AB,垂足为Q,PQ=10,∠B=30°,∠PAB=45°,以A为原点,AB所在的直线为x轴建立如图所示的坐标系.
(2013•唐山一模)如图,△ABC中,P是BC上一点,PQ⊥AB,垂足为Q,PQ=10,∠B=30°,∠PAB=45°,以A为原点,AB所在的直线为x轴建立如图所示的坐标系.| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
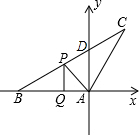
| AP |
| AC |
| PB |
| AB |
10
| ||
| AC |
| 20 | ||
10+10
|
| 2 |
| 3 |
| 2 |
| 6 |
| 2 |
| 6 |


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
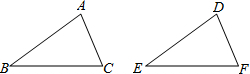 (2013•唐山一模)如图,给出下列四组条件:
(2013•唐山一模)如图,给出下列四组条件:查看答案和解析>>
科目:初中数学 来源:2011年重庆市綦江县赶水镇中中考数学模拟试卷(一)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com