
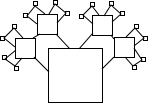
 一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图).若第1个正方形的边长是1,则生长到第4次后,所得图形的面积是________.
一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图).若第1个正方形的边长是1,则生长到第4次后,所得图形的面积是________.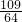
 、
、 、
、 ,
, ×
× ×
× ×2=
×2= ,
, ×
× ×
× ×4=
×4= ,
, ,
, 的面积,即剩
的面积,即剩  ,
,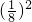 ×
× =
=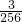 ,
,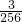 ×8=
×8=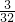 ,
, +
+ +
+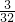 =1
=1 .
.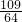 .
.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
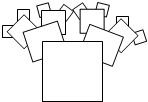 一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图所示)若第一个正方形的边长是1,则生长到第4次所得缺角正方形的面积是
一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图所示)若第一个正方形的边长是1,则生长到第4次所得缺角正方形的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
 的正方形.如图所示,由左图至右图,利用面积的不同表示方法写出一个代数恒等式是( )
的正方形.如图所示,由左图至右图,利用面积的不同表示方法写出一个代数恒等式是( )查看答案和解析>>
科目:初中数学 来源: 题型:
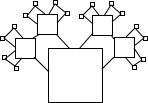 一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图).若第1个正方形的边长是1,则生长到第4次后,所得图形的面积是
一个纸质的正方形“仙人掌”,假设“仙人掌”在不断地生长,新长的叶子是“缺角的正方形”,这些“正方形”的中心在先前正方形的角上,它们的边长是先前正方形的一半(如图).若第1个正方形的边长是1,则生长到第4次后,所得图形的面积是| 109 |
| 64 |
| 109 |
| 64 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com