
当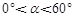 时,下列关系式中有且仅有一个正确.
时,下列关系式中有且仅有一个正确.
A.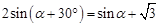
B.
C.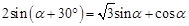
(1)正确的选项是 ;
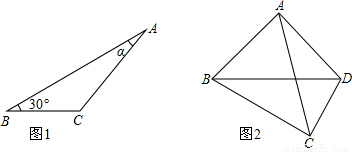
(2)如图1,△ABC中, 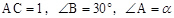 ,请利用此图证明(1)中的结论;
,请利用此图证明(1)中的结论;
(3)两块分别含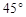 和
和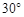 的直角三角板如图2方式放置在同一平面内,
的直角三角板如图2方式放置在同一平面内,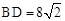 ,求
,求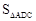 .
.
(1)C;(2)证明见解析;(3)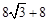 .
.
【解析】
试题分析:(1)先做(2),根据特殊元素法得出结论;(2)构造直角三角形,过A、C点作AD⊥BC交BC的延长线于点D,CE⊥AB于E,根据三角函数知识,可用α表示出AB的长度,再表示出AE和BE的长度,AB=AE+BE,分别让带有α两式相等即可;(3)要求三角形的面积,必须找到三角形的一边和这条边上的高;过点A作AG⊥CD交CD的延长线于G点.根据题意可知CD和AD的长度,和∠ADG的度数,根据上述得出的结论,可以求出∠的正弦值,在直角三角形ADG中,AD已知,根据三角函数关系式即可得出AG的长度,代入S△ADC的面积公式即可.
试题解析:(1)C.
(2)如图1,过点A作AD⊥BC交BC的延长线于点D.
∵∠B=30°,∠BAC=α,AC=1,∴∠ACD=α+30°.
∴在△ADC中,∠ADC=90°,AD=AC•sin∠ACD=sin(α+30°).
∵在△ABD中,∠ADB=90°,∠B=30°,∴AB=2AD=2sin(α+30°).
过点C作CE⊥AB于E.
∴在△CEA中,∠AEC=90°,CE=sinα,AE=cosα.
在△BEC中,∠BEC=90°, .
.
∴AB=AE+BE=cosα+
 .
.
∴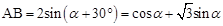 .
.

(3)由(2)证明的等式易得 .
.
如图2,过点A作AG⊥CD交CD的延长线于点G.
∵△ABD和△BCD是两个含45°和30°的直角三角形, ,∴∠ADG=75°,AD=8,CD=
,∴∠ADG=75°,AD=8,CD= .
.
∵ .
.
∴在△ADG中,∠AGD=90°,AG=AD•sin∠ADG=8×sin75°=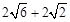 .
.
∴ .
.

考点:1.解直角三角形;2.三角形外角性质;3. 锐角三角函数定义;4.特殊角的三角函数值;5.三角形面积.


科目:初中数学 来源: 题型:
某汽车行驶时油箱中余油量Q(升)与行驶时间t(小时)的关系如下表:
![]()
(1)写出用行驶时间t表示余油量Q的代数式Q= ;
(2)当![]() 时,余油量Q的值为 ;
时,余油量Q的值为 ;
(3)汽车每小时行驶60公里,问油箱中原有汽油可供汽车行驶多少公里?
45.小虎一家利用元旦三天驾车到某景点旅游,小汽车出发前油箱有油36L,匀速行驶若干小时后,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题:
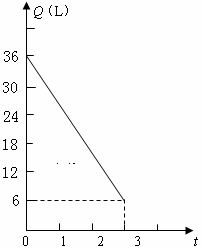
(1)求油箱余油量Q与行驶时间t之间的函数关系式;
(2)如果出发地距景点200km,车速为80km/h,要到达景点,油箱中的油是否够用?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
当![]() 时,下列关系式中有且仅有一个正确.
时,下列关系式中有且仅有一个正确.
A. ![]()
B. ![]()
C. ![]()
(1)正确的选项是 ;
(2)如图1,△![]() 中,
中, ![]() ,∠
,∠![]() =
=![]() ,
,![]() ,请利用此图证明(1)中的结论;
,请利用此图证明(1)中的结论;
(3)两块分别含![]() 的直角三角板如图2方式放置在同一平面内,
的直角三角板如图2方式放置在同一平面内,![]() =
=![]() ,求
,求![]() .
.
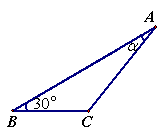

图1
图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com